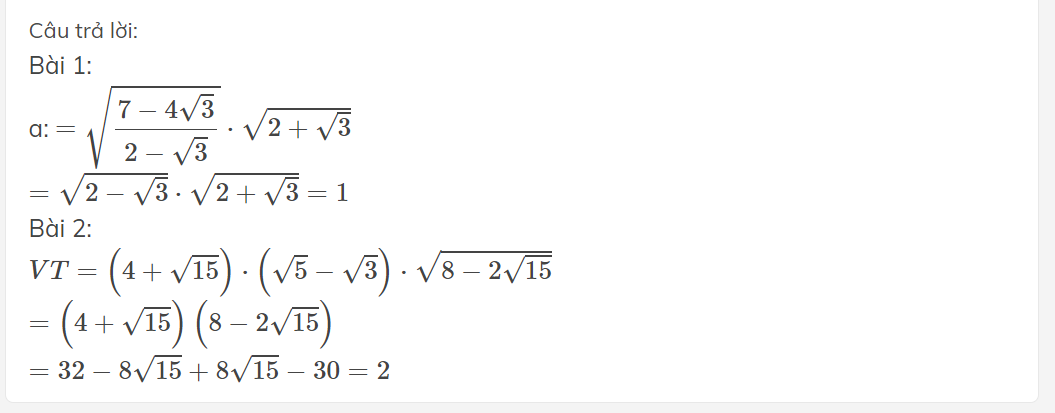Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c,\(\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a^2}-1+a}\right)\left(\sqrt{\frac{1}{a^2}-1}-\frac{1}{a}\right)\)
\(=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{\sqrt{1-a}.\sqrt{1-a}}{\sqrt{1-a}\left(\sqrt{1+a}-\sqrt{1-a}\right)}\right)\left(\frac{\sqrt{1-a^2}-1}{a}\right)\)
\(=\frac{\left(\sqrt{1+a}+\sqrt{1-a}\right)^2}{\left(1+a\right)-\left(1-a\right)}.\frac{\left(\sqrt{1-a^2}-1\right)}{a}=-1\)
M chỉ làm tiếp thôi nha, ko chép lại đề với đk đâu
a,
\(=\frac{a+2\sqrt{ab}+b-4\sqrt{ab}}{\sqrt{a}-\sqrt{b}}-\)\(\frac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\frac{a-2\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}-\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}-\sqrt{a}+\sqrt{b}\)
\(=\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}\)
\(=0\)
b,
\(=\left(a-b\right)\left(\sqrt{\frac{a+b}{a-b}}-1\right)\left(a-b\right)\left(\sqrt{\frac{a+b}{a-b}}+1\right)\)
\(=\left(a-b\right)^2\left(\frac{a+b}{a-b}-1\right)\)
\(=\left(a-b\right)^2\cdot\frac{a+b-a+b}{a-b}\)
\(=\left(a-b\right)2b=2ab-2b^2\)

\(D=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}-\frac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}\)
\(=\frac{a-2\sqrt{ab}+b+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\frac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\frac{a+2\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}-\frac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}-\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\sqrt{a}+\sqrt{b}-\sqrt{a}+\sqrt{b}\)
\(=2\sqrt{b}\)
\(D=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\frac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}\)
\(D=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\frac{-b+\sqrt{a}.\sqrt{b}}{\sqrt{b}}\)
\(D=\frac{\left[\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}\right].\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right).\sqrt{b}}-\frac{\left(\sqrt{a}.\sqrt{b}-b\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{b}.\left(\sqrt{a}+\sqrt{b}\right)}\)
\(D=\frac{\left[\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}\right]-\left(\sqrt{a}.\sqrt{b}-b\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{b}.\left(\sqrt{a}+\sqrt{b}\right)}\)
\(D=\frac{2b.\sqrt{a}+2b.\sqrt{b}}{\sqrt{b}.\left(\sqrt{a}+\sqrt{b}\right)}\)
\(D=\frac{2b.\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}\)
\(D=2\sqrt{b}\)

\(P=\frac{a+b}{\sqrt{a}+\sqrt{b}}:\left(\frac{a+b}{a-b}-\frac{\sqrt{b}}{\sqrt{b}-\sqrt{a}}+\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}\right)-\frac{\left|\sqrt{a}-\sqrt{b}\right|}{2}\)
\(P=\frac{a+b}{\sqrt{a}+\sqrt{b}}:\left(\frac{a+b}{a-b}+\frac{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{a-b}+\frac{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}{a-b}\right)-\frac{\left|\sqrt{a}-\sqrt{b}\right|}{2}\)
\(P=\frac{a+b}{\sqrt{a}+\sqrt{b}}:\left(\frac{a+b+\sqrt{ab}+b+a-\sqrt{ab}}{a-b}\right)-\frac{\left|\sqrt{a}-\sqrt{b}\right|}{2}\)
\(P=\frac{a+b}{\sqrt{a}+\sqrt{b}}:\left(\frac{2\left(a+b\right)}{a-b}\right)-\frac{\left|\sqrt{a}-\sqrt{b}\right|}{2}\)
\(P=\frac{\sqrt{a}-\sqrt{b}}{2}-\frac{\left|\sqrt{a}-\sqrt{b}\right|}{2}\)
TH1: \(a>b\Rightarrow P=\frac{\sqrt{a}-\sqrt{b}}{2}-\frac{\sqrt{a}-\sqrt{b}}{2}=0\)
TH2: \(0< a< b\Rightarrow P=\frac{\sqrt{a}-\sqrt{b}}{2}-\frac{\sqrt{b}-\sqrt{a}}{2}=\sqrt{a}-\sqrt{b}\)

Bài 1:
a: \(=\sqrt{\dfrac{7-4\sqrt{3}}{2-\sqrt{3}}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Bài 2:
\(VT=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

1)))))))
\(\frac{2}{\sqrt{ab}}:\left(\frac{1}{\sqrt{a}}-\frac{1}{\sqrt{b}}\right)^2-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)
\(=\frac{2}{\sqrt{ab}}:\frac{\left(\sqrt{b}-\sqrt{a}\right)^2}{\left(\sqrt{ab}\right)^2}-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)
\(=\frac{2}{\sqrt{ab}}.\frac{\left(\sqrt{ab}\right)^2}{\left(\sqrt{a}-\sqrt{b}\right)^2}-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)
\(=\frac{2\sqrt{ab}}{\left(\sqrt{a}-\sqrt{b}\right)^2}-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)
\(=\frac{2\sqrt{ab}-a-b}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)
\(=\frac{-\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}-\sqrt{b}\right)^2}=-1\)
\(\text{VT}=\left(1+\frac{x+\sqrt{x}}{\sqrt{x}+1}\right)\left(1-\frac{x-\sqrt{x}}{\sqrt{x}-1}\right)=\left(1+\frac{\sqrt{x}.\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right)\left(1-\frac{\sqrt{x}.\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right)\)
\(=\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)=1-x=\text{VP(điều phải chứng minh)}\)