Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số f(x) = xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=
.
Vậy
=
.
b) Hàm số f(x) = xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= -5.
Vậy
= -5.

\(lim_{x\rightarrow1}\frac{x^3+2x-3}{x^2-x}\)
\(=lim_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2+x+3\right)}{x\left(x-1\right)}\)
\(=lim_{x\rightarrow1}\frac{x^2+x+3}{x}\)
\(=\frac{1^2+1+3}{1}\)
\(=5\)
\(lim_{x\rightarrow1}\frac{\sqrt{2x+2}-\sqrt{3x+1}}{x-1}\)
\(=lim_{x\rightarrow1}\frac{\left(2x+2\right)-\left(3x+1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{2x+2-3x-1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-x+1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1\left(x-1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1}{\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=\frac{-1}{\sqrt{2\cdot1+2}+\sqrt{3\cdot1+1}}\)
\(=\frac{-1}{2+2}=\frac{-1}{4}\)

a)  (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) =  x4(1 -
x4(1 - 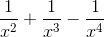 ) = +∞.
) = +∞.
b)  (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) =  x3(-2 +
x3(-2 + 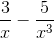 ) = +∞.
) = +∞.
c) 
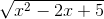 =
= 
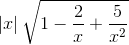 = +∞.
= +∞.
d) 
 =
= 

= 
 =
= 
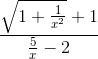 = -1.
= -1.

a) Học sinh tự vẽ hình. Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 - 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có f(x) =
(3x + 2) = 3(-1) +2 = -1.
f(x) =
(x2 - 1) = (-1)2 - 1 = 0.
Vì f(x) ≠
f(x) nên không tồn tại
f(x). Vậy hàm số gián đoạn tại
x0 = -1.

a)
=
= -4.
b)
=
=
(2-x) = 4.
c)
=
=
=
=
.
d)
=
= -2.
e)
= 0 vì
(x2 + 1) =
x2( 1 +
) = +∞.
f)
=
= -∞, vì
> 0 với ∀x>0.

Mình đăng nhầm