Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi năng suất ban đầu là x, thời gian ban đầu là y
Theo đề, ta có hệ: xy=120 và 2x+(x+4)(y-2-1)-16=120
=>xy=120 và 2x+(x+4)(y-3)=136
=>xy=120 và 2x+xy-3x+4y-12=136
=>xy=120 và -x+4y+120-12=136
=>-x+4y=28 và xy=120
=>x=4y-28 và y(4y-28)=120
=>y=10 và x=4*10-28=12

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 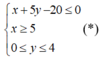
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
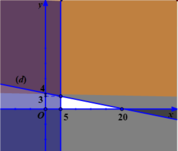
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

a) Gọi hàm số bậc hai cần tìm là: \(y = a{t^2} + bt + c.\)
Ta có: đỉnh \(I\left( {0;3,2} \right)\) và đi qua điểm \(\left( {1;4} \right)\)
nên \(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{{2a}} = 0}\\{c = 3,2}\\{a + b + c = 4}\end{array}} \right.\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{b = 0}\\{c = 3,2}\\{a + c = 4}\end{array}\,\,} \right. \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 0,8}\\{b = 0}\\{c = 3,2}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = 0,8{t^2} + 3,2\)
b) Thời gian từ năm 2018 đến năm 2024 là: \(t = 2024 - 2018 = 6\) năm
Số lượng máy tính xách tay bán được trong năm 2024 là:
\(0,{8.6^2} + 3,2 = 32\) nghìn chiếc
c) Năm bán đượng vượt mức 52 nghìn chiếc máy tính là:
\(\begin{array}{l}0,8{t^2} + 3,2 > 52\\ \Leftrightarrow \,\,0,8{t^2} - 48,8 > 0\\ \Leftrightarrow \,\,t \in \left( { - \infty ; - \sqrt {61} } \right) \cup \left( {\sqrt {61} ; + \infty } \right)\end{array}\)
Vì \(t > 0\) nên \(t \in \left( {\sqrt {61} ; + \infty } \right)\) hay \(t > \sqrt {61} \approx 7,8\).
Từ năm thứ 8 hay năm 2026 thì số lượng máy tính xách tay bán ra vượt mức 52 nghìn chiếc.

Gọi số sản phẩm làm theo kế hoạch là \(x\) (sản phẩm)
=> Số ngày dự định làm xong là: \(\frac{x}{25}\) (ngày)
Số sản phẩm làm được sau khi cải tiến kĩ thuật là: \(x+10\) (sản phẩm)
=> Số ngày làm xong là: \(\frac{x+10}{30}\) (ngày)
Ta có: \(\frac{x}{25}-\frac{x+10}{30}=3\)
Giải phương trình đi bạn :)