Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

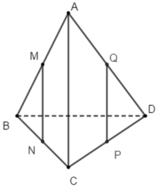
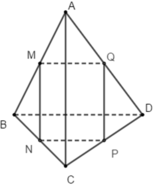
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và
M
N
=
1
2
A
C
(1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và Q P = 1 2 A C (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)

Đáp án C

Phương án A sai vì có thể xảy ra trường hợp giống câu 4 như hình sau:

Phương án B và C sai vì có thể sảy ra như hình sau.

Phương án D đúng vì: có thể ba vecto n → , a → , b → đồng phẳng hoặc không đồng phẳng như hai hình trên.
Đáp án D

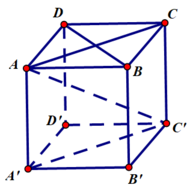
1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)