Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N P Q
+) Hình thang ABCD có M; N là trung điểm của AD; BC => MN là đường trung bình của hình thang
=> MN // AB // CD và MN = (AB + CD)/2
+) Tam giác ADB có MP // AB; M là trung điểm của AD => P là trung điểm của DB
Tam giác ABC có NQ // AB; N là trung điểm của BC => Q là trung điểm của AC
+) 2.MN = AB + CD => AB = 2.MN - CD = 2.6 - 8 = 4 cm
c) MP = AB/2 = 4/2 = 2 cm
QN = AB/2 = 4/2 = 2 cm
=> PQ = MN - MP - QN = 6 - 2 - 2 = 2 cm
ĐS:...
Chỉ hình thang ABCD (AB//CD). Phân giác góc A cắt BC tại E.
a) CM: AB=BE
b) Phân giác góc B cắt AE tại F. CMR: BF vuông góc với AE và FA.FE.
c) Gọi M,N lần lượt là trung điểm cua AB và CD. CMR: M,F,N thẳng hàng

a. M, N là trung điểm của AD, BC => MN là đường trung bình của hình thang ABCD
=> \(MN=\frac{AB+CD}{2}\Leftrightarrow2MN=AB+CD\Leftrightarrow AB=2MN-CD=2.6-8=4\)
b. Vì MN là đường trung bình của hình thang ABCD => MN//AB <=> MP//AB
Mà M là trung điểm AD => P là trung điểm của BD
=> MP là đường trung bình trong tam giác ABD => MP=1/2 AB=1/2.4=2
Làm tương tự, có: QN=1/2AB = 2
=> PQ = MN - MP - QN = 6 - 2 - 2 = 2

A B C D M N P Q H
a, Ta có: AM = MD (gt), BN=CN (gt)
=> MN là đường trung bình của hình thang ABCD
=>\(MN=\frac{AB+CD}{2}\Rightarrow AB+8=6.2\Rightarrow AB=12-8=4\left(cm\right)\)
b, MN là đường trung bình của hình thang ABCD
=> MN // AB
Mà AM = MD (gt)
=> MP là đường trung bình của t/g ABD
=> \(MP=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
Lại có: MN // AB, BN=CN(gt)
=>NQ là đường trung bình cuat t/g ABC
=>\(NQ=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
=> PQ = MN - MQ - NQ = 6 - 2 - 2 = 2 (cm)
Vậy...
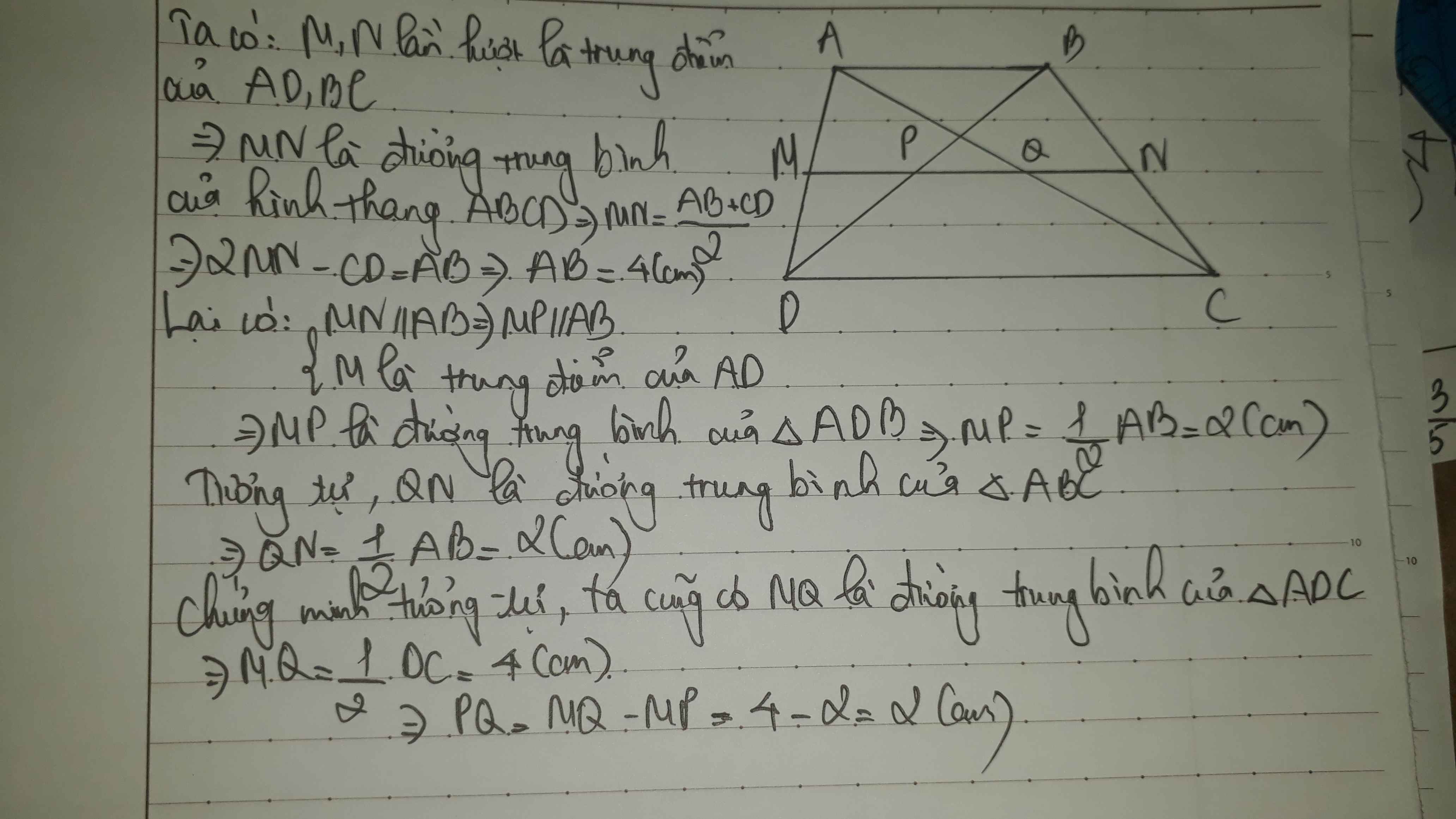
A B C D 8 cm 5cm M N P
a)Do MN //DC suy ra NP//DC
xét tam giác DBC có :
NP // DC ( cmt)
NB=NC ( gt)
\(\Rightarrow\)PB=PD ( định lí đảo đường TB tam giác )
Vậy PB= PD
b) Áp tính chất đường trung bình vào hình thang ABCD , ta có
MN = ( AB + DC )/ 2 = 13/2cm
Áp tính chất đường trung bình vào tam giác ADB, ta có
MP = AB / 2 = 8/ 2= 4cm
Vậy MN = 13/2 cm
MP = 4cm