Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0

2.
ĐK: \(2x-y\ge0;y\ge0;y-x-1\ge0;y-3x+5\ge0\)
\(\left\{{}\begin{matrix}xy-2y-3=\sqrt{y-x-1}+\sqrt{y-3x+5}\left(1\right)\\\left(1-y\right)\sqrt{2x-y}+2\left(x-1\right)=\left(2x-y-1\right)\sqrt{y}\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow\left(1-y\right)\sqrt{2x-y}+y-1+2x-y-1-\left(2x-y-1\right)\sqrt{y}=0\)
\(\Leftrightarrow\left(1-y\right)\left(\sqrt{2x-y}-1\right)+\left(2x-y-1\right)\left(1-\sqrt{y}\right)=0\)
\(\Leftrightarrow\left(1-\sqrt{y}\right)\left(\sqrt{2x-y}-1\right)\left(1+\sqrt{y}\right)+\left(\sqrt{2x-y}-1\right)\left(1-\sqrt{y}\right)\left(\sqrt{2x-y}+1\right)=0\)
\(\Leftrightarrow\left(1-\sqrt{y}\right)\left(\sqrt{2x-y}-1\right)\left(\sqrt{y}+\sqrt{2x-y}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=1\\y=2x-1\end{matrix}\right.\) (Vì \(\sqrt{y}+\sqrt{2x-y}+2>0\))
Nếu \(y=1\), khi đó:
\(\left(1\right)\Leftrightarrow x-5=\sqrt{-x}+\sqrt{-3x+6}\)
Phương trình này vô nghiệm
Nếu \(y=2x-1\), khi đó:
\(\left(1\right)\Leftrightarrow2x^2-5x-1=\sqrt{x-2}+\sqrt{4-x}\) (Điều kiện: \(2\le x\le4\))
\(\Leftrightarrow2x\left(x-3\right)+x-3+1-\sqrt{x-2}+1-\sqrt{4-x}=0\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{1+\sqrt{4-x}}-\dfrac{1}{1+\sqrt{x-2}}+2x+1\right)=0\)
Ta thấy: \(1+\sqrt{x-2}\ge1\Rightarrow-\dfrac{1}{1+\sqrt{x-2}}\ge-1\Rightarrow1-\dfrac{1}{1+\sqrt{x-2}}\ge0\)
Lại có: \(\dfrac{1}{1+\sqrt{4-x}}>0\); \(2x>0\)
\(\Rightarrow\dfrac{1}{1+\sqrt{4-x}}-\dfrac{1}{1+\sqrt{x-2}}+2x+1>0\)
Nên phương trình \(\left(1\right)\) tương đương \(x-3=0\Leftrightarrow x=3\Rightarrow y=5\)
Ta thấy \(\left(x;y\right)=\left(3;5\right)\) thỏa mãn điều kiện ban đầu.
Vậy hệ phương trình đã cho có nghiệm \(\left(x;y\right)=\left(3;5\right)\)
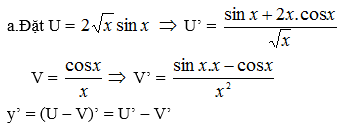
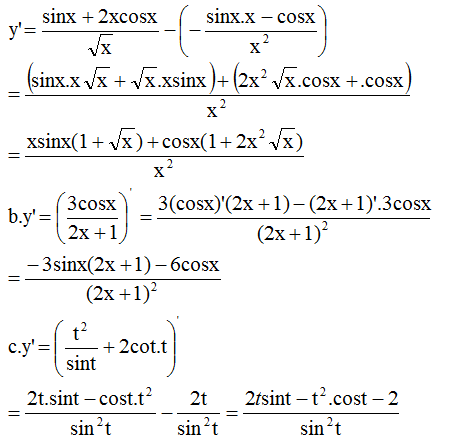
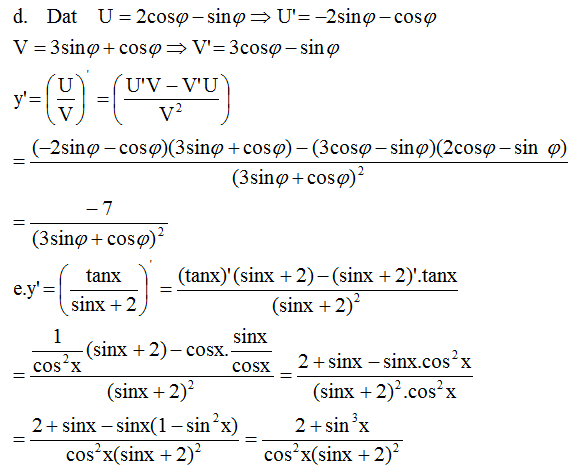
1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)