Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\left|y-18\right|\ge0\left(\forall y\right)\)
\(\Rightarrow A=\left|y-18\right|+7\ge7\)
Dấu "=" xảy ra <=>y - 18 = 0 <=> y = 18
Vậy AMin = 7 khi và chỉ khi y = 18
b) \(B=\left|y+2\right|-19\ge-19\)
Dấu "=" xảy ra <=> y + 2 = 0 <=> y = -2
Vậy BMin = -19 khi và chỉ khi y = -2
c) \(C=\left|y+8\right|+\left|y-30\right|=\left|y+8\right|+\left|30-y\right|\ge\left|y+8+30-y\right|=38\)
Dấu "=" xảy ra <=> \(\left(y+8\right)\left(30-y\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}y+8\ge0\\30-y\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}y\ge-8\\y\le30\end{cases}\Leftrightarrow-8\le}y\le30}\)
Vậy .....
d) Tương tự câu c

Ta biết rằng :\(|A|\ge A\)( Dấu "=" xảy ra khi và chỉ khi A \(\ge\) 0)
\(|A|=|-A|\) và \(|A|\ge0\)(Dấu ''='' xảy ra khi và chỉ khi A = 0)
Ta có: \(A=|x-3|+|x-5|+|x-7|\ge x-3+0+7-x=4\)
Dấu ''='' xảy ra khi và chỉ khi
\(\hept{\begin{cases}x-3\ge0\\x-5=0\\7-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge3\\x=5\Leftrightarrow x=5\\x\le7\end{cases}}}\)
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.

Ta có:
|x – 3| + |x – 7| = |x – 3| + |7 – x| ≥ |x – 3 + 7 – x| = |4| = 4.
(áp dụng bài 140: |x| + |y| ≥|x + y|)
* Lại có: |x – 5| ≥ 0.
Vậy A = |x – 3| + |x – 5| + |x – 7| ≥ 4 + 0 = 4.
Dấu ''='' xảy ra khi và chỉ khi: 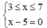 , tức là x = 5.
, tức là x = 5.
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.
\(A=\left|56-x\right|+\left|x+80\right|\)
Áp dụng bđt \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) ta có:
\(A\ge\left|56-x+x+80\right|=136\)
Vậy GTNN của A là 136 khi \(-80\le x\le56\)
Ta có : \(\begin{cases}\left|56-x\right|\ge56-x\\\left|x+80\right|\ge x+80\end{cases}\)\(\Rightarrow\left|56-x\right|+\left|x+80\right|\ge56-x+x+80\)
\(\Rightarrow\left|56-x\right|+\left|x+80\right|\ge136\)
Dấu " = " xảy ra khi \(\begin{cases}56-x\ge0\\x+80\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\le56\\x\ge-80\end{cases}\)
Vậy MINA=136 khi \(-80\le x\le56\)