XT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
QD
24 tháng 4 2017
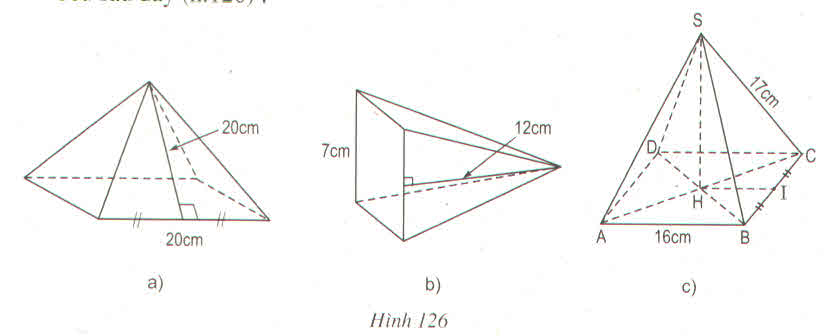
Hình a : Sxq = p.d = \(\dfrac{1}{2}\).20.4.20 = 800(cm2)
Diện tích đáy: Sđ = 202 = 400(cm2)
Diện tích toàn phần của lăng trụ hai là:
Stp = Sxq + Sđ = 800 + 400 = 1200(cm2)
Hình b: Sxq = p.d = \(\dfrac{1}{2}\).7.4.12 = 168(cm2)
Sđ = 72 = 49(cm2)
Stp = Sxq + Sđ = 168 + 49 = 217(cm2)
Hình c: Chiều cao của mặt bên của hình chóp:
\(h=\sqrt{17^2-8^2}=\sqrt{225}=15\left(cm\right)\)
Sxq = p.d = \(\dfrac{1}{2}\).16.4.15 = 480(cm2)
Sđ = 162 = 256(cm2)
Stp = Sxq + Sđ = 480 + 256 = 736(cm2)
28 tháng 9 2017
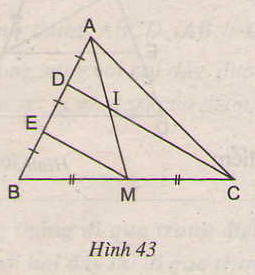
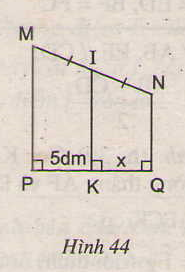
t/g DBC có :
ED = EB ( gt )
MB = MC ( gt )
Nên EM là đường trung bình của tam giác DBC
\(\Rightarrow\)EM // DC
T/g AEM có :
DA = DE ( gt )
DI // EM ( cmt , vì EM // DC )
Theo định lý 1 ta có :
AI = IM ( đpcm )
QD
24 tháng 4 2017
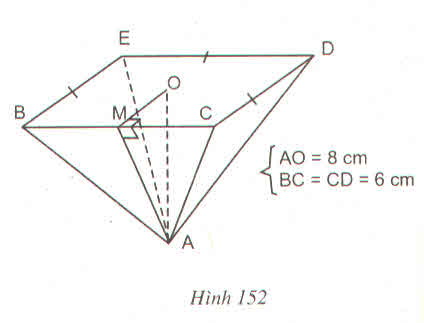
a) Diện tích đáy của hình chóp đều:
S = BC 2 = 6,52 = 42,25 (m2)
Thể tích hình chóp đều:
V = \(\dfrac{1}{3}\). S.h = \(\dfrac{1}{3}\). 42,25 . 12 ≈ 169 (cm3)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5cm. Nên:
Sxq = \(4.\dfrac{\left(2+4\right).3,5}{2}=42\left(cm^2\right)\) = 42 (cm2)
18 tháng 2 2017
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
18 tháng 2 2017
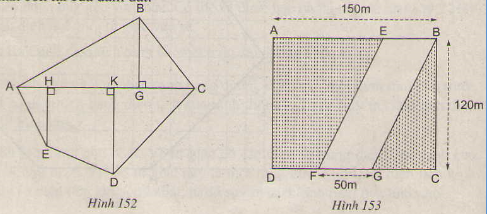
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
CD
30 tháng 9 2017
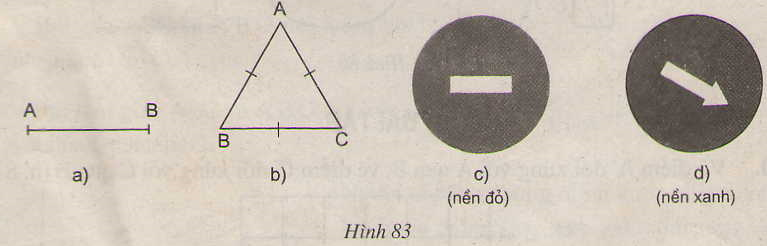
Hình 83a, c có tâm đối xứng.
Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB,
Hình 83c có tâm đối xứng là tâm của đường tròn.
PT
1
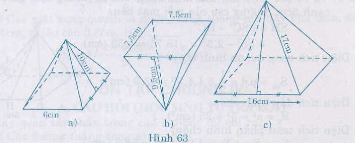
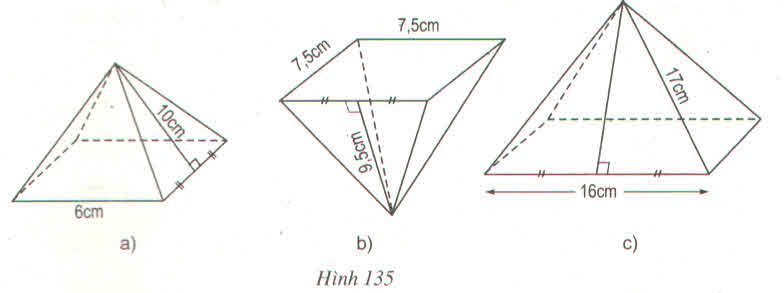
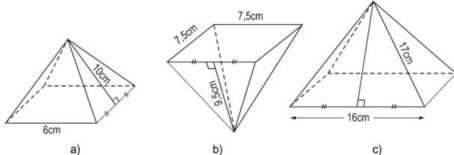
Hình a: Sxq = p.d = 1212.6.4. 10 = 120 (cm2)
Hình b: Sxq = p.d = 1212.7,5 .4. 9,5 =142,5 (cm2)
Hình c: Độ dài trung đoạn:
d = √172−82172−82 = √289−64289−64 = √225 = 15(cm)
Nên Sxq = p.d = 1212.16.4.15 =480 (cm2)