K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
12 tháng 11 2021
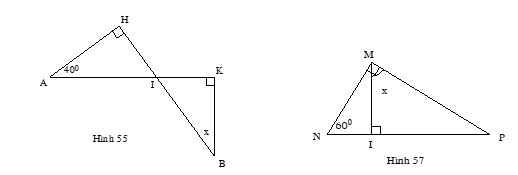
Hình 55:
Xét tam giác AHI và tam giác BKI lần lượt vg tại H,K có:
\(\left\{{}\begin{matrix}\widehat{HAI}+\widehat{HIA}=90^0\\x+\widehat{KIB}=90^0\end{matrix}\right.\)
Mà \(\widehat{HIA}=\widehat{KIB}\)(đối đỉnh)
\(\Rightarrow x=\widehat{HAI}=40^0\)
Hình 57:
Xét tam giác MNP vg tại M và tam giác MIP vg tại I:
\(\left\{{}\begin{matrix}\widehat{N}+\widehat{NMI}=90^0\\x+\widehat{NMI}=90^0\end{matrix}\right.\)
\(\Rightarrow x=\widehat{N}=60^0\)
HZ
2
28 tháng 9 2017
a) A+B+C=180 độ (tổng ba góc của tam giác)
90 độ +55 độ + x=180 đ
145 độ +x=180
x=180-145
x=35
LT
tìm tọa độ hình tạo bởi các điểm M(x,y) thỏa mãn từng điều kiện sau:
a. |x| +|y| =1
b. x/|x| +y/|y|= 2
0
11 tháng 7 2019
1a) \(0,31:0,91=x:\frac{49}{3}\)
=> \(\frac{0,31}{0,91}=\frac{3x}{49}\)
=> \(3x=\frac{3}{7}.49\)
=> \(3x=21\)
=> \(x=21:3=7\)
b) \(6,88:x=12:27\)
=> \(\frac{6,88}{x}=\frac{12}{27}\)
=> \(x=6,88:\frac{4}{9}\)
=> \(x=15,48\)
c) \(\frac{25}{3}:\frac{35}{3}=13:2x\)
=> \(\frac{13}{2x}=\frac{5}{7}\)
=> \(2x=13:\frac{5}{7}\)
=> \(2x=\frac{91}{5}\)
=> \(x=\frac{91}{5}:2=\frac{91}{10}\)
d) \(\left(x-1\right):24,5=5:8,75\)
=> \(\frac{x-1}{24,5}=\frac{5}{8,75}\)
=> \(x-1=\frac{4}{7}.24,5\)
=> \(x-1=14\)
=> \(x=14+1=15\)
11 tháng 7 2019
2a) Ta có: \(\frac{x}{y}=\frac{5}{7}\) => \(\frac{x}{5}=\frac{y}{7}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5}=\frac{y}{7}=\frac{x+y}{5+7}=\frac{4,08}{12}=0,34\)
=> \(\hept{\begin{cases}\frac{x}{5}=0,34\\\frac{y}{7}=0,34\end{cases}}\) => \(\hept{\begin{cases}x=0,34.5=1,7\\y=0,34.7=2,38\end{cases}}\)
Vậy x = 1,7; y = 2,38
b) Ta có: \(\frac{x}{y}=-\frac{3}{7}\) => \(\frac{x}{-3}=\frac{y}{7}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{-3}=\frac{y}{7}=\frac{x-y}{-3-7}=\frac{-40}{-10}=4\)
=> \(\hept{\begin{cases}\frac{x}{-3}=4\\\frac{y}{7}=4\end{cases}}\) => \(\hept{\begin{cases}x=4.\left(-3\right)=-12\\y=4.7=28\end{cases}}\)
vậy x = -12; y = 28
c) Ta có: \(\frac{x}{y}=\frac{3}{5}\) => \(\frac{x}{3}=\frac{y}{5}\)
Đặt : \(\frac{x}{3}=\frac{y}{5}=k\) => \(\hept{\begin{cases}x=3k\\y=5k\end{cases}}\) (*)
Khi đó, ta có: xy = 1215
hay 3k. 5k = 1215
=> 15k2 = 1215
=> k2 = 1215 : 15 = 81
=> k = \(\pm\)9
Thay k = \(\pm\)9 vào (*), ta được:
+) x = 3. (\(\pm\)9) = \(\pm\)27
+) y = 5. (\(\pm\)9) = \(\pm\)45
Vậy ...
NN
0
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
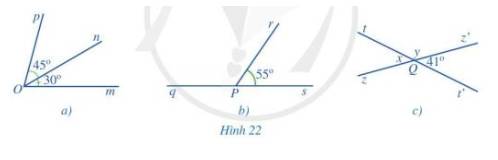
a) Vì tia On nằm trong góc mOp nên \(\widehat {mOn} + \widehat {nOp} = \widehat {mOp}\)
\(\begin{array}{l} \Rightarrow 30^\circ + 45^\circ = \widehat {mOp}\\ \Rightarrow 75^\circ = \widehat {mOp}\end{array}\)
Vậy số đo góc mOp là 75 độ
b) Ta có: \(\widehat {q\Pr } + \widehat {rPs} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {q\Pr } + 55^\circ = 180^\circ \\ \Rightarrow \widehat {q\Pr } = 180^\circ - 55^\circ = 125^\circ \end{array}\)
Vậy số đo góc qPr là 125 độ
c) Ta có: \(\widehat {tQz} = \widehat {t'Qz'}\) ( 2 góc đối đỉnh), mà \(\widehat {t'Qz'} = 41^\circ \Rightarrow \widehat {tQz} = 41^\circ \)
\(\widehat {tQz'} + \widehat {z'Qt'} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tQz'} + 41^\circ = 180^\circ \Rightarrow \widehat {tQz'} = 180^\circ - 41^\circ = 139^\circ \)
Vậy x = 41 \(^\circ \) ; y = 139 \(^\circ \)
TT
2
5 tháng 2 2021
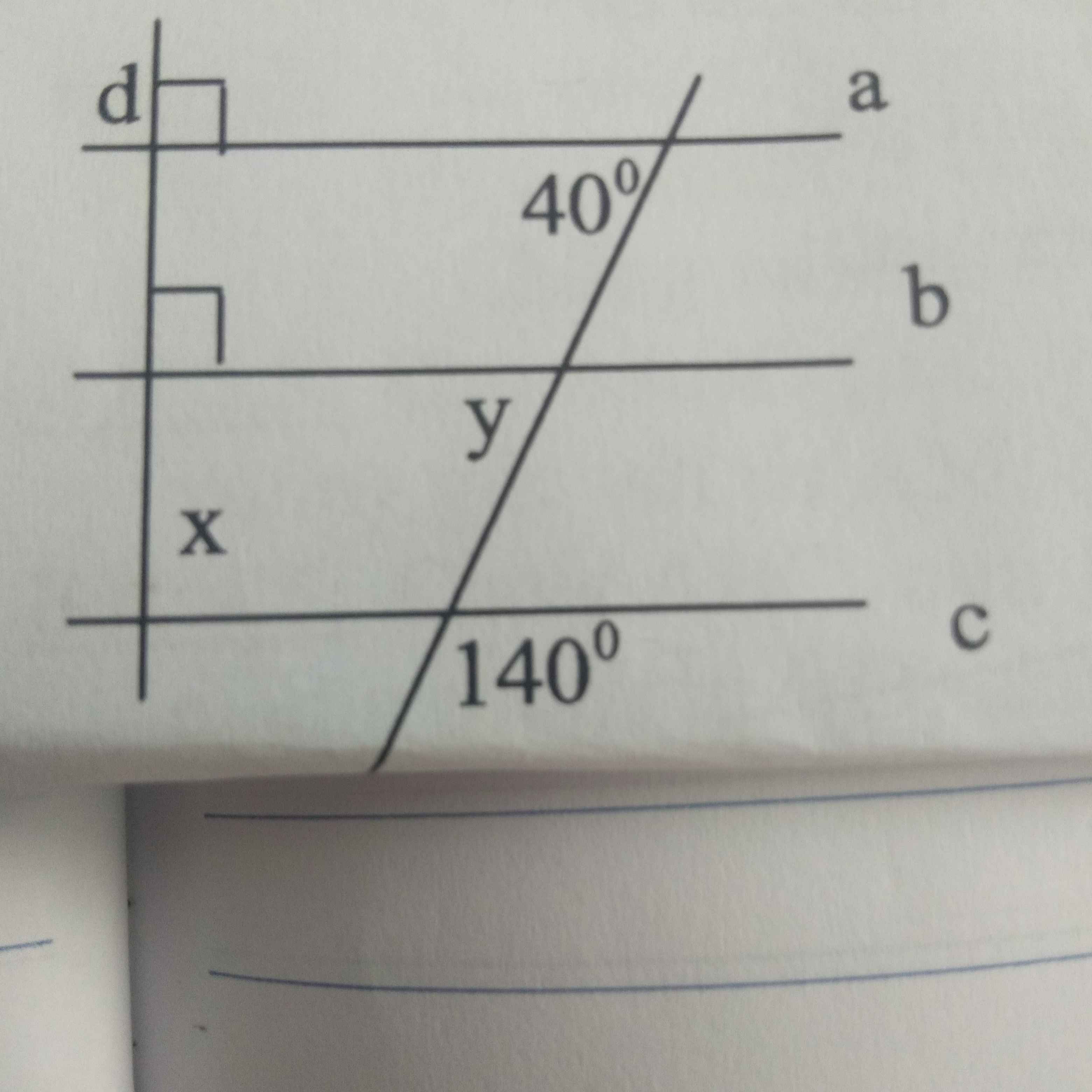
Đề có cho thêm dữ kiện gì không bạn? Vì nếu hình như thế này thì không tìm được x,y
LH
0