K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2022
a, \(\Rightarrow x-2\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x-2 | 1 | -1 | 3 | -3 |
| x | 3 | 1 | 5 | -1 |
b, \(3\left(x-2\right)+13⋮x-2\Rightarrow x-2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
| x-2 | 1 | -1 | 13 | -13 |
| x | 3 | 1 | 15 | -11 |
c, \(x\left(x+7\right)+2⋮x+7\Rightarrow x+7\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x+7 | 1 | -1 | 2 | -2 |
| x | -6 | -8 | -5 | -9 |
2 tháng 4 2020
\((x-6)(3x-9)>0\)
TH1:
\(\orbr{\begin{cases}x-6< 0\\3x-9< 0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x< 6\\x< 3\end{cases}}\)\(\Rightarrow x< 3\)
TH2:
\(\orbr{\begin{cases}x-6>0\\3x-9>0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x>6\\x>3\end{cases}}\)\(\Rightarrow x>6\)
Vậy \(x< 3\) hoặc \(x>6\)thì \((x-6)(3x-9)>0\)
Học tốt!
2 tháng 4 2020
20.
\((2x-1)(6-x)>0\)
TH1:
\(\orbr{\begin{cases}2x-1>0\\6-x>0\end{cases}\Rightarrow\orbr{\begin{cases}x< \frac{1}{2}\\x< 6\end{cases}}\Rightarrow x< 6}\)
TH2
\(\orbr{\begin{cases}2x-1< 0\\6-x< 0\end{cases}\Rightarrow\orbr{\begin{cases}x>\frac{1}{2}\\x>6\end{cases}}\Rightarrow x>\frac{1}{2}}\)
Vậy \(x< 6\)hoặc \(x>\frac{1}{2}\)thì \((2x-1)(6-x)>0\)
VH
1
20 tháng 3 2020
a) (x2-1)(x2-4)<0
=> x2-1 và x2-4 trái dấu nhau
Ta thấy: x2 >=0 với mọi x => x2-1 > x2-4
=> \(\hept{\begin{cases}x^2-1>0\\x^2-4< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2>1\\x^2< 4\end{cases}\Leftrightarrow}\hept{\begin{cases}x>\pm1\\x< \pm2\end{cases}}}\)
=> Không có giá trị củ x thỏa mãn đề bài
SC
1
18 tháng 1 2015
a) 3 . ( 2 - x ) + 5 . ( x - 6 ) = -98
6 - 3x + 5x - 30 = -98
6 + 2x -30 = -98
6 + 2x = -98 + 30
6 + 2x = -68
2x = -68 -6
2x = -74
x = -74 : 2
x = -37
PT
1
TM
1
S
26 tháng 2 2022
Cho phương trình: x^2 -2(m+1)x + 4m=0a．Chứng minh rằng phương trình luôn luôn có no với mọi mb．Giari phương trình khi m=2c．Tìm m để phương trình
Cho phương trình: x^2 -2(m+1)x + 4m=0 a．Chứng minh rằng phương trình luôn luôn có no với mọi m b．Giari phương trình khi m=2 c．Tìm m để phương trình có 1no x= -2 ѵà tìm no còn lại d．Tìm k để x1^2 + x2^2 = 5
Đáp:
NT
2
4 tháng 3 2020
\(a,0< x< 5\)
\(=>1\le x\le4\)
\(=>x\in\left\{1;2;3;4\right\}\)
\(b,0\le x< 4\)
\(=>0\le x\le3\)
\(=>x\in\left\{0;1;2;3\right\}\)
\(c,-1< x\le4\)
\(=>0\le x\le4\)
\(=>x\in\left\{0;1;2;3;4\right\}\)
\(d,-2< 2x\)
\(=>x>-1\)
\(=>x\ge0\)
\(=>x\inℕ\)
\(e,0< x-1\le2\)
\(=>1\le x-1\le2\)
\(=>x-1\in\left\{1;2\right\}\)
\(=>x\in2;3\)
4 tháng 3 2020
a. 0 < x < 5
=> \(x\in\left\{1;2;3;4\right\}\)
vậy...............................
b. 0 < x < 4
\(\Rightarrow x\in\left\{0;1;2;3\right\}\)
Vậy,,,,,,,,,,,,,,,,,,,,,,,,,,,,.....
c. -1 < x < 4
\(\Rightarrow x\in\left\{0;1;2;3;4\right\}\)
Vậy..................................
e. 0 < x - 1 < 2
=> 0-1 < x-1 < 2-1
=> -1 < x < 1
=> x=0
Vậy x=0
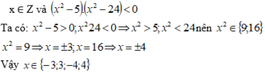
quên!
thanks mate