Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Bình có 2 khả năng thắng cuộc:
+) Thắng cuộc sau lần quay thứ nhất. Nếu Bình quay vào một trong 5 nấc: 80, 85, 90, 95, 100 thì sẽ thắng nên xác suất thắng cuộc của Bình trường hợp này là P 1 = 5 20 = 1 4
+) Thắng cuộc sau 2 lần quay. Nếu Bình quay lần 1 vào một trong 15 nấc: 5, 10, ..., 75 thì sẽ phải quay thêm lần thứ 2. Ứng với mỗi nấc quay trong lần thứ nhất, Bình cũng có 5 nấc để thắng cuộc trong lần quay thứ 2, vì thế xác suất thắng cuộc của Bình trường hợp này là P 2 = 15 × 5 20 × 20 = 3 16
Từ đó, xác suất thắng cuộc của Bình là
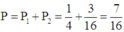

Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là 1 12 .

Không gian mẫu: \(n\left(\Omega\right)=10!\)
Chọn 5 chữ số từ 6 chữ số còn lại (khác 0,3,6,8): có \(C_6^5\) cách
Hoán vị 6 chữ số (5 chữ số được chọn nói trên và số 8): \(6!\) cách
Tổng cộng: \(6!.C_6^5\) số
Xác suất: \(P=\dfrac{6!.C_6^5}{10!}=...\)

Tham khảo:
Số phần tử của không gian mẫu là ![]() . Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:
. Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:
TH1: Người đó gọi đúng ở lần thứ nhất.
TH2: Người đó gọi đúng ở lần thứ hai. Gọi A1 người đó gọi đúng ở lần thứ nhất
![]() Xác suất người đó gọi đúng là P(A1) = \(\dfrac{1}{10}\)
Xác suất người đó gọi đúng là P(A1) = \(\dfrac{1}{10}\)
Xác suất người đó gọi không đúng là P(A1) = \(\dfrac{9}{10}\).
Gọi A2 là người đó gọi đúng ở lần thứ hai
![]() Xác suất người đó gọi đúng là P(A2) = \(\dfrac{1}{9}\) .
Xác suất người đó gọi đúng là P(A2) = \(\dfrac{1}{9}\) .
Gọi A là người đó gọi đúng số điện thoại mà không phải thử quá hai lần, ta có ![]()
 (đpcm)
(đpcm)

Chọn D
Gọi 2 số cuối là ab,là số điện thoại nên có đủ các chữ số từ 0 đến 9
Ta có a có 10 cách chọn, b khác a nên có 9 cách chọn. Vậy không gian mẫu có 9.10= 90 phần tử.
Vậy xá xuất gọi một lần dúng là 1/90



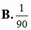

khó vậy