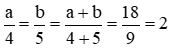Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S_{Xq}=\left(12+8+\sqrt{12^2+8^2}\right)\cdot10=\left(20+4\sqrt{13}\right)\cdot10\left(cm^2\right)\)

Lời giải:
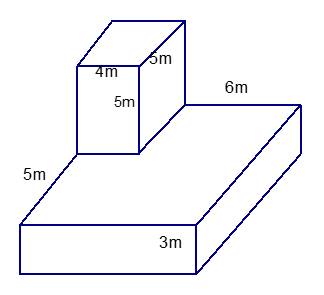
a. Thể tích hồ bơi: $25\times 10\times 2,2=550$ (m3)
b. Tổng diện tích các mặt trong lòng hồ:
$25\times 10+2\times 2,2\times (25+10)=404$ (m2)
c.
Thể tích nước trong hồ: $2\times 25\times 10=500$ (m3)
Số tiền mua nước:
$500\times 6869=3434500$ (đồng)

Gọi độ dài chiều rộng và chiều dài của hình chữ nhật lần lượt là a, b (m) (a, b > 0)
Theo đề bài ta có: 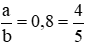
Suy ra: 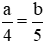
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra: a = 8; b = 10
Độ dài chiều rộng và chiều dài của hình chữ nhật lần lượt là 8m và 10m
Vậy diện tích của hình chữ nhật là: 8.10=80m2

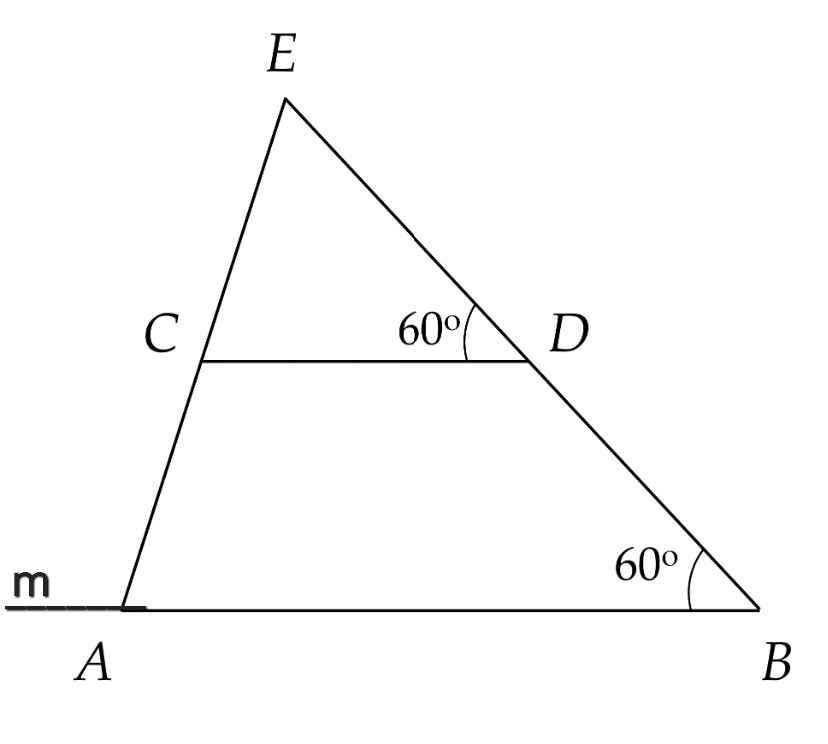
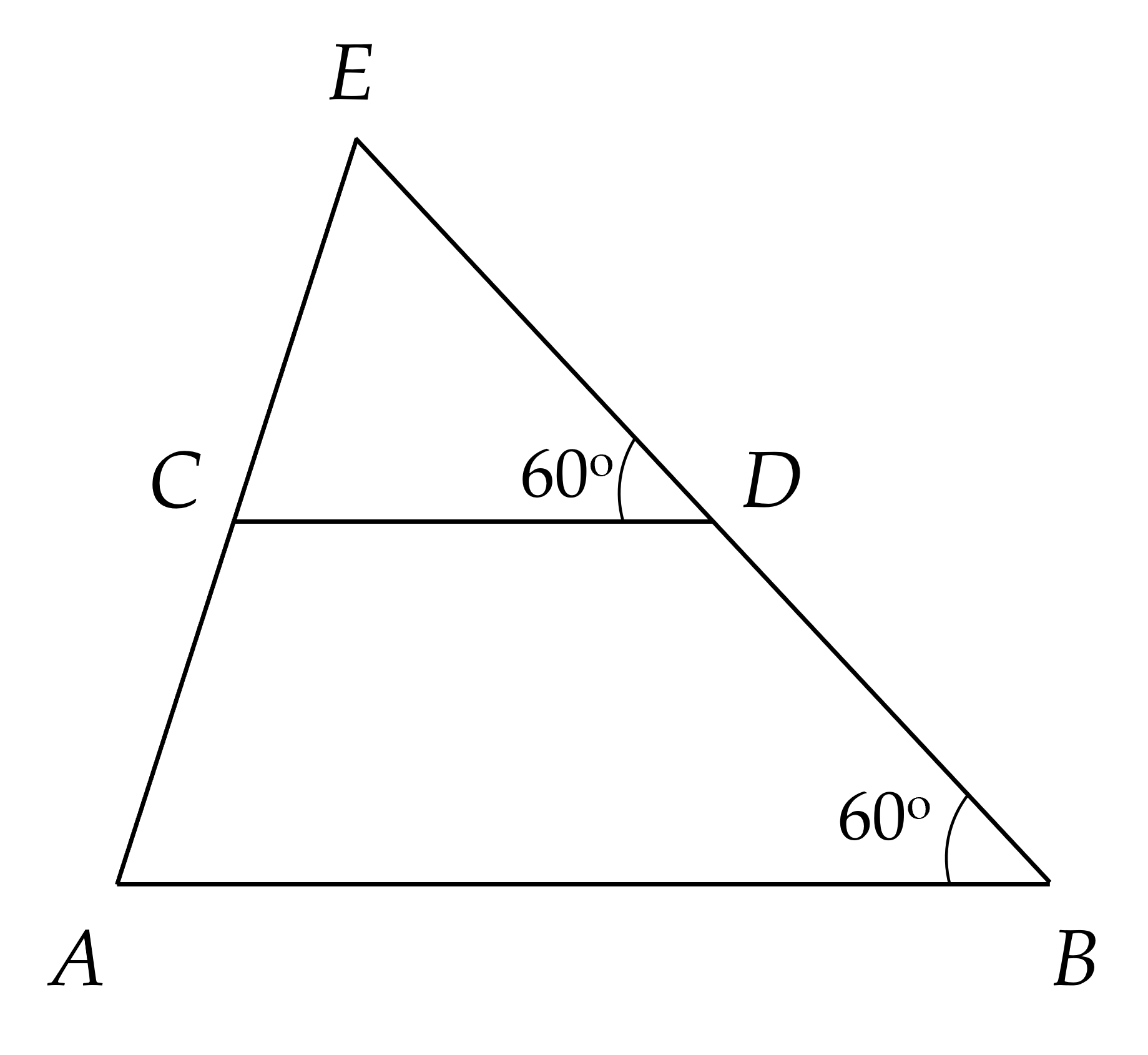
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Gọi hai kích thước của hình chữ nhật đó lần lượt là a và b
\(\Rightarrow\frac{a}{3}=\frac{b}{5}\) và a . b = 24
Đặt \(\frac{a}{3}=\frac{b}{5}=k\Rightarrow\hept{\begin{cases}a=3k\\b=5k\end{cases}}\)
\(\Rightarrow a.b=3k.5k=8k=24\)
\(\Rightarrow k=3\Rightarrow\hept{\begin{cases}a=3.4=12\left(m\right)\\b=5.4=20\left(m\right)\end{cases}}\)
Chu vi hình chữ nhật đó là :
( 12 + 20 ) . 2 = 64 ( m )
Đáp số : 64 m

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

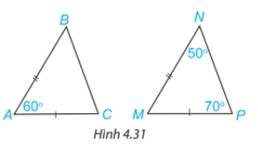
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)