Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Thấu kính này là TLHT vì ảnh ngược chiều vs vật...cho ảnh thật,,...
b. hình tự vẽ...
f= OF = OF'= 4.8 cm

a) vì là TKHT mà theo đề thì ta có d (tức là OA) < f ,=> ảnh ảo, cùng chiều và lớn hơn vật
b)Xét tam giác OAB đồng dạng vs ta, giác OA'B'
=> h/h' = d/d' (AB/A'B'=OA/OA')..........(1)
xét tam giac F'OI đồng dạng vs tgiac F'A'B'
=> h/h' = f/(f+d') (( OI/A'B' = FO/(FO+FA')))..........(2)
từ 1 và 2 => d/d' =f/(f+d')
chia 2 vế cho dd'f => 1/d =1/f + 1/d'
theo đề có d và f => d'=12
thế d'=12, d=6, h=1 vào (1)
=>h'=2
F' A O A' B' I

a, Vẽ ảnh A'B'
A B A' B' F F' O I
b,
Gọi khoảng cách từ AB đến thấu kính là d, từ A'B' đến thấu kính là d'
Xét \(\Delta ABO \sim \Delta A'B'O\)
\(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{BO}{B'O}=\dfrac{10}{d'}\)(1)
Xét \(\Delta IOF \sim \Delta A'B'F\)
\(\Rightarrow \dfrac{IO}{A'B'}= \dfrac{OF}{B'F}\)
Ta có: \(IO=AB\)
\(\Rightarrow \dfrac{AB}{A'B'}= \dfrac{14}{d'+14}\)(2)
Từ (1) và (2) \(\Rightarrow\dfrac{10}{d'}=\dfrac{14}{d'+14}\)
\(\Rightarrow d'=35cm\)
Vậy ảnh cách thấu kính 35 cm
Thế vào (1) ta được: \(\Rightarrow \dfrac{AB}{A'B'}=\dfrac{10}{35}\Rightarrow A'B' = \dfrac{35.2}{10}=7(cm)\)
Vậy ảnh cao 7cm.

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

Tiêu điểm của kính luôn nằm trên truc chính. Vì thấu kính phân kì cho tia ló đi qua tiêu điểm, do đó đường kéo dài cắt truc chính tai 1 điểm, điểm đó chính là tiêu điểm. Vì tiêu điểm có khoảng cách đến quang tâm O là 15cm nên tiêu cư của thấu kính là 15 cm --> đáp án A
2. C. Bằng phép dùng chứng minh tam giác đồng dang ta sẽ có đươc 2 tam giác của ảnh và vât bằng nhau

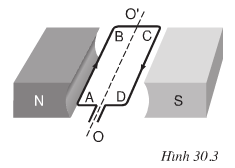
a)Xem hình 30.3b
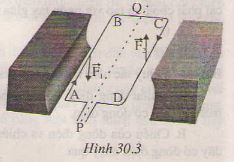
b) Cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) làm cho khung dây quay ngược chiều kim đồng hồ.
c)Khung dây quay theo chiều ngược lại khi cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) có chiều ngược lại, muốn vậy phải đổi chiều dòng điện trong khung dây hoặc phải đổi chiều từ trường.

Khoảng cách ảnh AB tới thấu kính \(d_2\):
\(\dfrac{1}{f_2}=\dfrac{1}{d_2}+\dfrac{1}{d_2'}\Rightarrow d_2'=\dfrac{d_2\cdot f_2}{d_2-f_2}=\dfrac{9d_2}{d_2-9}\left(cm\right)\)
Di chuyển thấu kính lại gần màn ảnh 24 cm:
\(\Rightarrow d_2"=\dfrac{\left(d_2+24\right)\cdot f_2}{d_2+24-f_2}=\dfrac{9\left(d_2+24\right)}{d_2+15}\left(cm\right)\)
Khoảng cách giữa ảnh AB và O1 là:
\(d_2+\dfrac{9d_2}{d_2-9}=d_2+24+\dfrac{9\left(d_2+24\right)}{d_2+15}\)
\(\Rightarrow d_2^2+6d_2-216=0\Rightarrow\left[{}\begin{matrix}d_2=12cm\\d_2=-18cm\left(loại\right)\end{matrix}\right.\)
Ảnh AB cách thấu kính O1:
\(d_1'=60-12-36=12cm\)
Tiêu cự thấu kính O1:
\(\dfrac{1}{f_1}=\dfrac{1}{d_1}+\dfrac{1}{d_1'}=\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{6}\)
\(\Rightarrow f_1=6cm\)
Tịnh tiến AB trước thấu kính O để ảnh độ cao không phụ thuộc vào vị trí của vật.
Xảy ra\(\Leftrightarrow\)Tiêu điểm hai thấu kính trùng nhau.
\(\Leftrightarrow O_1O_2=f_1+f_2=6+9=15cm\)