Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔSAC có
H,I lần lượt là trung điểm của SA,SC
=>HI là đường trung bình
=>HI//AC
mà \(AC\subset\left(ABCD\right)\); HI không thuộc (ABCD)
nên HI//(ABCD)
b: Xét ΔSCD có
I,K lần lượt là trung điểm của SC,SD
=>IK là đường trung bình
=>IK//CD
mà \(CD\subset\left(ABCD\right);IK\) không thuộc (ABCD)
nên IK//(ABCD)
c: IK//(ABCD)
HI//(ABCD)
\(IK,HI\subset\left(HIK\right)\)
Do đó: (HIK)//(ABCD)

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)

a: XétΔCAS có
I,H lần lượt là trung điểm của CA,CS
=>IH là đường trung bình
=>IH//SA
mà \(SA\subset\left(SAB\right)\); IH không thuộc mp(SAB)
nên IH//(SAB)
Xét ΔSCD có
H,K lần lượt là trung điểm của SC,SD
=>HK là đường trung bình của ΔSCD
=>HK//CD
mà CD//AB
nên HK//AB
mà \(AB\subset\left(SAB\right)\) và HK không thuộc mp(SAB)
nên HK//(SAB)
HK//(SAB)
IH//(SAB)
\(HK,IH\subset\left(HIK\right)\)
Do đó: (HIK)//(SAB)
b: HK//CD
\(CD\subset\left(ABCD\right)\)
HK không thuộc mp(ABCD)
Do đó; HK//(ABCD)

a: Xét ΔSAD có
\(\dfrac{SM}{SA}=\dfrac{SP}{SD}=\dfrac{1}{2}\)
nên MP//AD
MP//AD
AD\(\subset\)(ABCD)
MP không nằm trong mp(ABCD)
Do đó: MP//(ABCD)
Xét ΔSAB có \(\dfrac{SM}{SA}=\dfrac{SN}{SB}=\dfrac{1}{2}\)
nên MN//AB
MN//AB
\(AB\subset\left(ABCD\right)\)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
MP//(ABCD)
MN//(ABCD)
MN,MP cùng nằm trong mp(MNP)
Do đó: (MNP)//(ABCD)
b: Xét ΔSDB có \(\dfrac{DP}{DS}=\dfrac{DI}{DB}\)
nên PI//SB
PI//SB
SB\(\subset\)(SBC)
PI không nằm trong mp(SBC)
Do đó: PI//(SBC)
Xét ΔASC có \(\dfrac{AI}{AC}=\dfrac{AM}{AS}=\dfrac{1}{2}\)
nên MI//SC
MI//SC
SC\(\subset\)(SBC)
MI không nằm trong mp(SBC)
Do đó: MI//(SBC)
PI//(SBC)
MI//(SBC)
MI,PI cùng nằm trong mp(MPI)
Do đó: (SBC)//(MPI)

a: Xét ΔSAD có M,P lần lượt là trung điểm của SA,SD
=>MP là đường trung bình
=>MP//AD
mà \(AD\subset\left(ABCD\right)\) và MP không thuộc mp(ABCD)
nên MP//(ABCD)
Xét ΔSBD có
N,P lần lượt là trung điểm của SB,SD
=>NP là đường trung bình
=>NP//BD
mà \(BD\subset\left(ABCD\right)\) và NP không thuộc mp(ABCD)
nên NP//(ABCD)
NP//(ABCD)
MP//(ABCD)
NP,MP\(\subset\left(MNP\right)\)
Do đó: (MNP)//(ABCD)
b: Xét ΔDBS có
P,I lần lượt là trung điểm của DS,DB
=>PI là đường trung bình
=>PI//SB
mà \(SB\subset\left(SBC\right)\) và PI không thuộc mp(SBC)
nên PI//(SBC)
MP//AD
AD//BC
Do đó: MP//BC
mà \(BC\subset\left(SBC\right)\) và MP không thuộc mp(SBC)
nên MP//(SBC)
MP//(SBC)
PI//(SBC)
MP,PI\(\subset\)(MPI)
Do đó: (MPI)//(SBC)

a: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình cuả ΔSAB
=>MN//AB
MN//AB
AB\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔSCB có
N,P lần lượt là trung điểm của SB,SC
=>NP là đường trung bình của ΔSBC
=>NP//BC
NP//BC
BC\(\subset\)(ABCD)
NP không nằm trong mp(ABCD)
Do đó: NP//(ABCD)
c: NP//(ABCD)
MN//(ABCD)
MN,NP nằm trong mp(MNP)
Do đó: (MNP)//(ABCD)
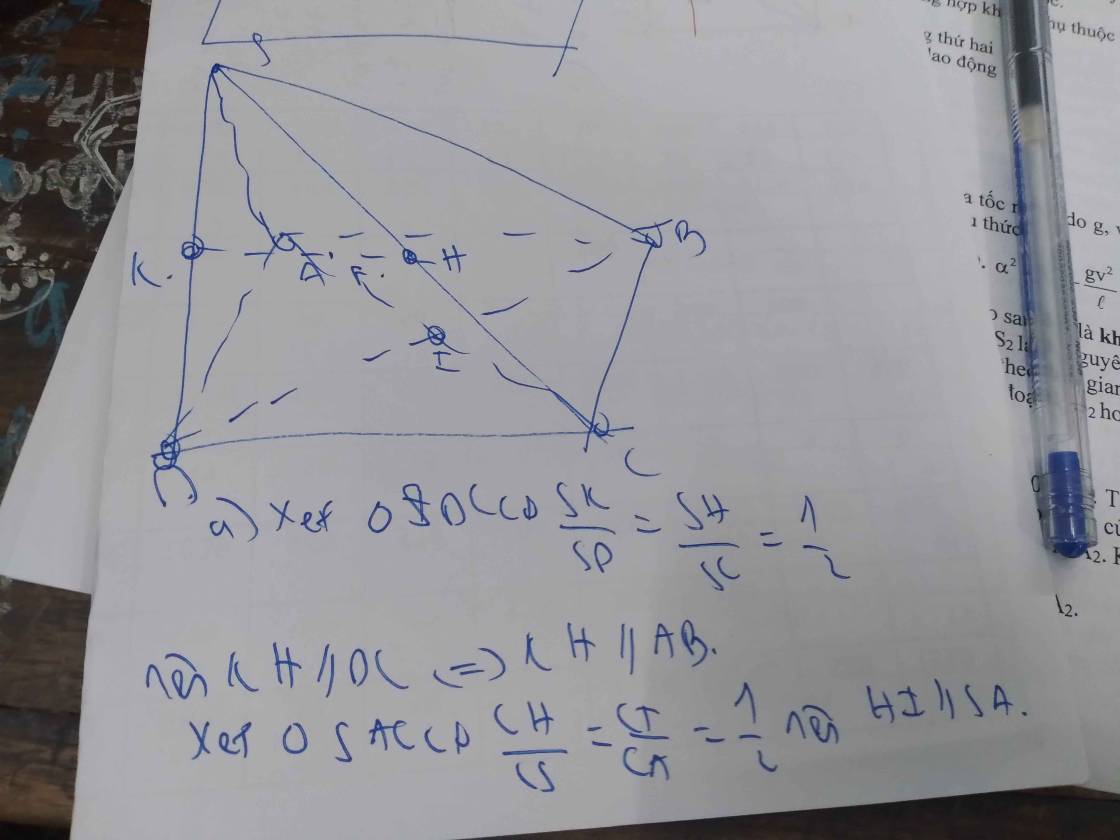
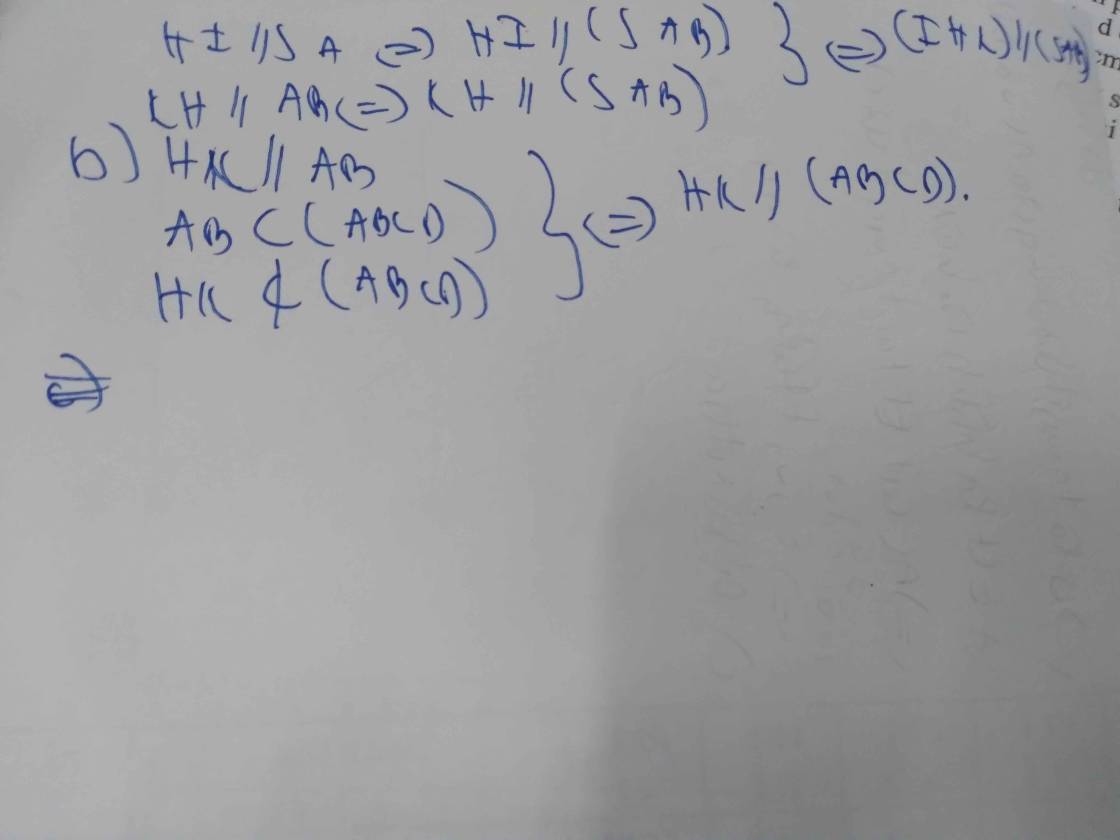

a: Xét ΔSAC có
I,H lần lượt là trung điểm của SC,SA
=>IH là đường trung bình của ΔSAC
=>IH//AC
IH//AC
AC\(\subset\)(ABCD)
IH không nằm trong mp(ABCD)
Do đó: IH//(ABCD)
b: XétΔSCD có
I,K lần lượt là trung điểm của SC,SD
=>IK là đường trung bình của ΔSCD
=>IK//CD
IK//CD
CD\(\subset\)(ABCD)
IK không nằm trong mp(ABCD)
Do đó: IK//(ABCD)
c: IK//(ABCD)
HI//(ABCD)
IK,HI nằm trong mp(HIK)
Do đó: (HIK)//(ABCD)
d: (HIK)//(ABCD)
=>BD//(HIK)