DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 12 2020
a, \(\sqrt{x^4-8x^2+16}=2-x\)ĐK : \(x\ge-2\)
\(\Leftrightarrow\sqrt{\left(x^2-4\right)^2}=2-x\Leftrightarrow\left(x-2\right)\left(x+2\right)=-\left(x-2\right)\)
\(\Leftrightarrow\left(x-2\right)\left[x+2+1\right]=0\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\Leftrightarrow x=2;-3\)
Theo ĐKXĐ Suy ra : \(x=2\)
b, tương tự
M
12 tháng 4 2018
a) Chứng minh tích BD.CEBD.CE không đổi.
Xét hai tam giác: ΔBOD∆BOD và ΔCEO∆CEO, ta có: ˆB=ˆC=600B^=C^=600 (gt) (1)
Ta có ˆDOCDOC^ là góc ngoài của ΔBDO∆BDO nên: ˆDOC=ˆB+ˆD1DOC^=B^+D^1
hay ˆO1+ˆO2=ˆB+ˆD1⇔600+ˆO2=600+ˆD1O1^+O2^=B^+D1^⇔600+O2^=600+D1^
⇔ˆO2=ˆD1(2)⇔O2^=D1^(2)
Từ (1) và (2) ⇒ΔBOD⇒∆BOD đồng dạng ΔCEO∆CEO (g.g)
⇒BDBO=COCE⇒BD.CE=BO.CO⇒BDBO=COCE⇒BD.CE=BO.CO
hay BD.CE=BC2.BC2=BC24BD.CE=BC2.BC2=BC24 (không đổi)
Vậy BD.CE=BC24BD.CE=BC24 không đổi
b) Chứng minh ΔBODΔBOD đồng dạng ΔOEDΔOED
Từ câu (a) ta có: ΔBOD∆BOD đồng dạng ΔCEO∆CEO
⇒ODOE=BDOC=BDOB⇒ODOE=BDOC=BDOB (do OC=OBOC=OB)
Mà ˆB=ˆDOE=600B^=DOE^=600
Vậy ΔBODΔBOD đồng dạng ΔOEDΔOED (c.g.c) ⇒ˆBDO=ˆODE⇒BDO^=ODE^
hay DODO là tia phân giác của góc BDEBDE
c) Vẽ OK⊥DEOK⊥DE và gọi II là tiếp điểm của (O)(O) với ABAB, khi đó OI⊥ABOI⊥AB. Xét hai tam giác vuông: IDOIDO và KDOKDO, ta có:
DODO chung
ˆD1=ˆD2D1^=D2^ (chứng minh trên)
Vậy ΔIDOΔIDO = ΔKDOΔKDO⇒OI=OK⇒OI=OK
Điều này chứng tỏ rằng OKOK là bán kính của (O)(O) và OK⊥DEOK⊥DE nên KK là tiếp điểm của DEDE với (O)(O)hay DEDE tiếp xúc với đường tròn (O)
19 tháng 10 2021
TL
+) Sử dụng định lí Pytago trong tam giác vuông: ΔABCΔABC vuông tại AA, khi đó: BC2=AC2+AB2BC2=AC2+AB2.
+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền:
b2=a.b′, c2=a.c′b2=a.b′, c2=a.c′
Lời giải chi tiết
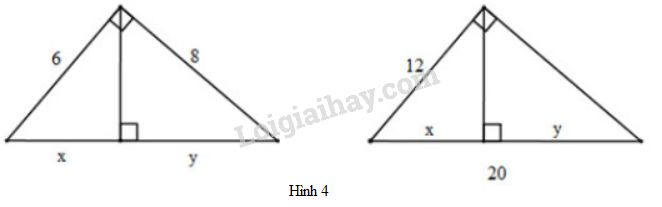
a) Đặt tên các đỉnh của tam giác như hình dưới:
Áp dụng định lí Pytago vào ΔABCΔABC vuông tại AA, ta có:
BC=√AB2+AC2=√62+82=10BC=AB2+AC2=62+82=10
Áp dụng hệ thức lượng vàoΔABCΔABC vuông tại AA, đường cao AHAH, ta có:
AB2=BC.BH⇒BH=AB2BC=6210=3,6AB2=BC.BH⇒BH=AB2BC=6210=3,6
Lại có HC=BC−BH=10−3,6=6,4HC=BC−BH=10−3,6=6,4
Vậy x=BH=3,6x=BH=3,6; y=HC=6,4y=HC=6,4.
b) Đặt tên các đỉnh của tam giác như hình dưới
Áp dụng hệ thức lượng vào ΔABCΔABC vuông tại AA, đường cao AHAH, ta có:
AB2=BH.BC⇔122=20.x⇒x=12220=7,2AB2=BH.BC⇔122=20.x⇒x=12220=7,2
Lại có: HC=BC−BH=20−7,2=12,8HC=BC−BH=20−7,2=12,8
Vậy x=BH=7,2;x=BH=7,2; y=HC=12,8y=HC=12,8.
Ht ông bn
19 tháng 10 2021
TL
Theo định lí Pitago ta có:
Áp dụng định lí 1 ta có:
- Hình b
Áp dụng định lí 1 ta có:
=> y = 20 - 7,2 = 12,8
Hoktot~
điều kiện \(\left\{{}\begin{matrix}x\ge0\\x\ne2\end{matrix}\right.\)
Ta thấy \(2\sqrt{x}\ge0\) với mọi \(\left\{{}\begin{matrix}x\ge0\\x\ne2\end{matrix}\right.\)
Nên để \(A< 0\) thì \(x-2< 0\) \(\Leftrightarrow x< 2\)
Như vậy để \(A< 0\) thì \(0\le x< 2\)