Mạch điện xoay chiều gồm biến trở,cuộn dây và tụ điện ghép nối tiếp.Đặt vào hai đầu đ...">
K
Khách

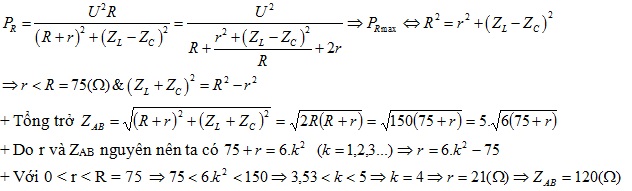
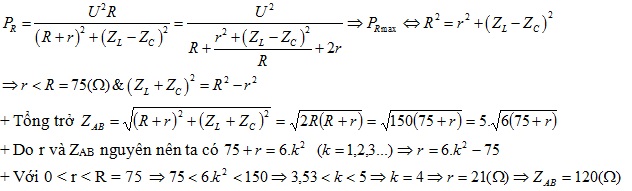
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
TK
Tui Không Có Tên
23 tháng 8 2016
Cho mạch điện xoay RLC nối tiếp.  là cường độ dòng điện qua mạch và  là hiệu điện thế giữa hai đầu đoạn mạch. Hiện tượng cộng hưởng xảy ra...
Đọc tiếp

Cho mạch điện xoay RLC nối tiếp. i = I_0 cos \omega t là cường độ dòng điện qua mạch và u = U_0 cos (\omega t + \varphi ) là hiệu điện thế giữa hai đầu đoạn mạch. Hiện tượng cộng hưởng xảy ra khi: 

A. RC = L

B. \frac{1}{LC\omega ^2} = 1

C. LC\omega = R^2

D. LC\omega^2 = R^2
#Vật lý lớp 12
1
LU
lưu uyên
23 tháng 8 2016

Hiện tượng cộng hưởng xảy ra khi
Z_L = Z_C \Leftrightarrow \omega L = \frac{1}{\omega C}
\Rightarrow \frac{1}{LC\omega ^2}= 1

Đúng(0)
TA
Thành An
25 tháng 1 2016
Cho đoạn mạch RLC với  đặt vào hai đầu đoạn mạch trên điện áp xoay chiều  (với U không đổi,  ω thay đổi được). Khi  và  thì mạch có cùng hệ số công suất, giá trị hệ số công suất đó...
Đọc tiếp

Cho đoạn mạch RLC với L/C=R^{2} đặt vào hai đầu đoạn mạch trên điện áp xoay chiều u=U\sqrt{2}cos\omega t (với U không đổi,  ω thay đổi được). Khi \omega =\omega _{1} và \omega =\omega _{2}=9\omega _{1} thì mạch có cùng hệ số công suất, giá trị hệ số công suất đó là

A. 3/\sqrt{73}                       B.   2/\sqrt{13}                     C.  2/\sqrt{21}                      D.4/\sqrt{64}

 
#Vật lý lớp 12
2
HD
Hoàng Đình Trọng Duy
25 tháng 1 2016

 

Đúng(0)
DM
Đặng Minh Triều
25 tháng 1 2016

Đúng(0)
NN
Nguyễn Ngọc Hà Phương
24 tháng 8 2016
Cho đoạn mạch nối tiếp theo thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn dây có độ tự cảm L, điện trở r. Biết . Đặt vào đoạn mạch điện áp xoay chiều  thì điện áp hiệu dụng của đoạn mạch RC gấp  lần điện áp hiệu dụng hai đầu cuộn dây. Hệ số công suất của đoạn mạch...
Đọc tiếp

Cho đoạn mạch nối tiếp theo thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn dây có độ tự cảm L, điện trở r. Biết L = CR^2 = Cr^2. Đặt vào đoạn mạch điện áp xoay chiều u = U\sqrt{2}cos\omega t (V) thì điện áp hiệu dụng của đoạn mạch RC gấp \sqrt{3} lần điện áp hiệu dụng hai đầu cuộn dây. Hệ số công suất của đoạn mạch là

 

A. 0,866.

B. 0,657. 

C. 0,785. 

D. 0,5. 
#Vật lý lớp 12
2
LN
Lê Nguyên Hạo
24 tháng 8 2016

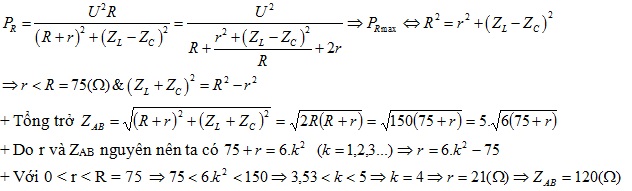
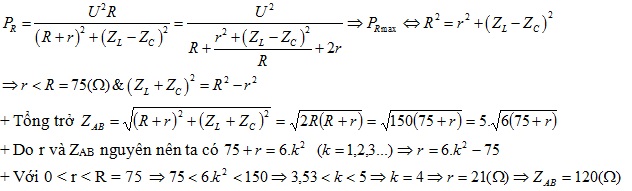
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)

\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)

Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)

A đúng

Đúng(0)
LU
lưu uyên
24 tháng 8 2016

Ta có: L = R^2 C = r^2 C
\Rightarrow Z_L. Zc = R^2 = r^2

Điện áp hiệu dụng của đoạn mạch RC gấp \sqrt{3} lần điện áp hiệu dụng hai đầu cuộn dây 
I. \sqrt{R^2 + Z_c^2} = \sqrt{3}.I. \sqrt{r^2 + Z_L^2}\Leftrightarrow R^2 + Z_c^2 = 3 (r^2 + Z_L^2)
\Leftrightarrow Z_L.Zc + Z_c^2 = 3.Z_L.Zc + 3 Z_L^2
\Leftrightarrow Zc(Z_L + Zc) = 3 Z_L (Z_L + Zc)
\Rightarrow Zc = 3Z_L \Rightarrow R^2 = 3 Z_L^2 \Rightarrow R = Z_L\sqrt{3}
=> Hệ số công suất của đoạn mạch là
cos \varphi = \frac{R + r}{\sqrt{(R + r)^2 + (Z_L - Zc)^2}} = \frac{2R}{\sqrt{4R^2 + 4 Z_L^2}} = \frac{2\sqrt{3}Z_L}{\sqrt{4.3. Z_L^2 + 4 Z_L^2}} = \frac{\sqrt{3}}{2}

Đúng(0)
HT
Hạ Thiên Mỹ
1 tháng 12 2016
Mạch điện xoay chiều gồm biến trở, cuộn dây và tụ điện ghép nối tiếp.Đặt vào 2 đầu đoạn mạch điện áp có biểu thức : u= U\(\sqrt{2}\)\(\cos\left(\omega t\right)\) (V) ( với U,\(\omega\) không đổi ) . Khi biến trở có giá trị R= 75 (\(\Omega\)) thì công suất tiêu thụ trên biến trở đạt giá trị lớn nhất. Xác định điện trở thuần cuộn dây và tổng trở của mạch AB ( Biết rằng chúng đều có...
Đọc tiếp

Mạch điện xoay chiều gồm biến trở, cuộn dây và tụ điện ghép nối tiếp.Đặt vào 2 đầu đoạn mạch điện áp có biểu thức : u= U\(\sqrt{2}\)\(\cos\left(\omega t\right)\) (V) ( với U,\(\omega\) không đổi ) . Khi biến trở có giá trị R= 75 (\(\Omega\)) thì công suất tiêu thụ trên biến trở đạt giá trị lớn nhất. Xác định điện trở thuần cuộn dây và tổng trở của mạch AB ( Biết rằng chúng đều có giá trị nguyên)

A: r= 15(\(\Omega\)) ; Z\(_{AB}\) =100((\(\Omega\))

B:r=21 (\(\Omega\)) ;Z\(_{AB}\)=120(\(\Omega\))

C:r=12(\(\Omega\)) ;Z\(_{AB}\) = 157(\(\Omega\))

 

D:r=35(\(\Omega\)) ;Z\(_{AB}\)= 150(\(\Omega\))

 
#Vật lý lớp 12
1
AH
Akai Haruma
Giáo viên
13 tháng 12 2016

Công suất tiêu thụ của biến trở:

$P_R=\frac{U^2R}{(R+r)^2+(Z_L-Z_C)^2}=\frac{U^2}{R+\frac{r^2+(Z_L-Z_C)^2}{R}+2r}\leq \frac{U^2}{2\sqrt{r^2+(Z_L-Z_C)^2}+2r}$

Do đó, $P_R$ đạt giá trị lớn nhất khi $R=\sqrt{(Z_L-Z_c)^2+r^2}\Leftrightarrow Z_{AB}^2=75^2+(75+r)^2-r^2$

Giờ chỉ cần thử các giá trị nguyên ta thu được $r=21\Omega$ và $Z_{AB}=120\Omega$, tức đáp án $B$ là đáp án đúng.

Đúng(3)
TA
Thành An
25 tháng 1 2016
Một cuộn dây không thuần cảm nối tiếp với tụ điện có điện dung C thay đổi được trong mạch điện xoay chiều có điện áp  . Ban đầu dung kháng ZC và tổng trở ZLr của cuộn dây và Z của toàn mạch đều bằng 100Ω. Tăng điện dung thêm một lượng  thì tần số dao động riêng của mạch này khi đó là 80. Tần số  ω của nguồn điện xoay chiều bằngA. 40π (rad/s)             ...
Đọc tiếp

Một cuộn dây không thuần cảm nối tiếp với tụ điện có điện dung C thay đổi được trong mạch điện xoay chiều có điện áp u=U_{0}cos\omega t(V) . Ban đầu dung kháng ZC và tổng trở ZLr của cuộn dây và Z của toàn mạch đều bằng 100Ω. Tăng điện dung thêm một lượng \Delta C=0,125.10^{-3}/\pi (F) thì tần số dao động riêng của mạch này khi đó là 80\pi (rad/s). Tần số  ω của nguồn điện xoay chiều bằng

A. 40π (rad/s)                B. 100 π (rad/s)              C. 80π (rad/s)                 D. 50π (rad/s)
#Vật lý lớp 12
2
DM
Đặng Minh Triều
25 tháng 1 2016

Từ ĐK đầu bài ta có: Zc^{2}=r^{2}+Zl^{2}=r^{2}+(Zl-Zc)^{2}\Rightarrow Zc=2Zl=100\Rightarrow \omega ^{2}=\frac{1}{2LC}
tần số dao động riwwng của mạch là:(80\Pi )^{2}=\frac{1}{L(C-\Delta C)}\Rightarrow L.C-L\Delta C=\frac{1}{80^{2}.10}\Rightarrow \frac{1}{2\omega^{2}}-\frac{50}{\omega }.\frac{0,125.10^{-3}}{\Pi }=\frac{1}{80^{2}.10}
giải phương trình bâc 2 này ra ta được: \omega =40\Pi

Đúng(0)
HD
Hoàng Đình Trọng Duy
25 tháng 1 2016

Z=Z_{C}=Z_{Lr}=100\Omega

Z_{C}=2Z_{L}\Rightarrow \frac{1}{\omega C}=2\omega L\Rightarrow \frac{1}{LC}=2\omega ^{2}(1)

{\omega _{0}}^{2}=\frac{1}{L(C+\Delta C)}(2)

Lấy (1) chia (2) ta được:  \frac{2\omega ^{2}}{{\omega _{0}}^{2}}=\frac{C+\Delta C}{C}

 

Đúng(0)
CC
Công Chúa Băng Giá
23 tháng 8 2016
ổng hợp hai dao động điều hào cùng...
Đọc tiếp

ổng hợp hai dao động điều hào cùng phương x_1 = 4 cos (\omega t - \frac{\pi}{6}) cm; x_2 = 4 sin (\omega t)(cm) là?

 

A. x = 4 cos (\omega t - \frac{\pi}{3}) cm

B. x = 4 \sqrt{3}cos (\omega t - \frac{\pi}{4}) cm

C. x = 4\sqrt{3}cos (\omega t - \frac{\pi}{3}) cm

D. x = 4cos (\omega t - \frac{\pi}{3}) cm
#Vật lý lớp 12
1
LU
lưu uyên
23 tháng 8 2016

x_1 = 4 cos (\omega t - \frac{\pi}{6}) cm; x_2 = 4 sin (\omega t )(cm)
x_1 = 4 cos (\omega t - \frac{\pi}{6}) cm; x_2 = 4 cos (\omega t - \frac{\pi}{2})(cm)
Sử dụng MTBT \Rightarrow x = 4\sqrt{3}cos (\omega t - \pi/3)cm

chọn C

Đúng(0)
MD
Minh Đức
29 tháng 5 2016
Cho mạch điện xoay chiều gồm một cuộn dây có hệ số tự cảm L = H và có điện trở thuần r = 10 mắc nối tiếp với một tụ điện có điện dung   C = mF. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số f = 50Hz và điện áp hiệu dụng U = 100V, pha ban đầu bằng 0. .Biểu thức của dòng điện qua mạch. Mọi ng giải chi tiết hô...
Đọc tiếp

Cho mạch điện xoay chiều gồm một cuộn dây có hệ số tự cảm L = \frac{0,1}{\pi }H và có điện trở thuần r = 10 mắc nối tiếp với một tụ điện có điện dung   C = \frac{500}{\pi }mF. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số f = 50Hz và điện áp hiệu dụng U = 100V, pha ban đầu bằng 0. .Biểu thức của dòng điện qua mạch. Mọi ng giải chi tiết hô với
 
#Vật lý lớp 12
1
NQ
Nguyễn Quang Hưng
29 tháng 5 2016

Bài này thì có vẹo gì đâu bạn.

\(u=100\sqrt 2\cos(100\pi t)(V)\)

\(Z_L=\omega L = 10\Omega\)

\(Z_C=\dfrac{1}{\omega C}=20\Omega\)

Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)

\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)

\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)

Suy ra: \(\varphi=\dfrac{\pi}{4}\)

Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Đúng(0)
MD
Minh Đức
29 tháng 5 2016
Cho mạch điện hình vẽ  , biết: R = 40Ω ,  và:; .  r và L có giá trị...
Đọc tiếp

Cho mạch điện hình vẽ  , biết: R = 40Ω , C=\frac{2,5}{\pi }.10^{-4}F

 và:u_{AM}=80cos100\pi t(V);u_{MB}=200\sqrt{2}cos(100\pi t+\frac{7\pi }{12})(V); .  r và L có giá trị là



 
#Vật lý lớp 12
1
NQ
Nguyễn Quang Hưng
29 tháng 5 2016

Hình đâu bạn ơi.

Đúng(0)
TT
trần thị phương thảo
24 tháng 5 2015
mạch điện xoay chiều mắc nối tiếp gồm cuộn cảm thuần L,tụ điện C,điện trở R.Đặt vào 2 đầu đoạn mạch 1 điện áp xoay chiều u=Uocos(wt) V ,Uo ko đổi ,w thay đổi được.Điều chỉnh w thì thấy khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng I= I max.Cho L=1/ H,w1-w2=150 tìm giá trị R...
Đọc tiếp

mạch điện xoay chiều mắc nối tiếp gồm cuộn cảm thuần L,tụ điện C,điện trở R.Đặt vào 2 đầu đoạn mạch 1 điện áp xoay chiều u=Uocos(wt) V ,Uo ko đổi ,w thay đổi được.Điều chỉnh w thì thấy khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng I=\frac{1}{\sqrt{5}} I max.Cho L=1/\Pi H,w1-w2=150\Pi tìm giá trị R của mạch điện
A R=37,5\Omega
B R=75\Omega
C R=150 \Omega
D R=50\Omega
#Vật lý lớp 12
1
NQ
Nguyễn Quang Hưng
25 tháng 5 2015

khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng

nên \(\omega_0^2=\omega_1\omega_2=\frac{1}{LC}\Rightarrow\omega_2L=\frac{1}{\omega_1C}\Rightarrow Z_{L2}=Z_{C1}\)

\(I_{max}=\frac{U}{R}\)

\(I=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}\)

Theo giả thiết: \(I=\frac{I_{max}}{\sqrt{5}}\)

\(\Rightarrow\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}=\frac{U}{\sqrt{5}R}\Rightarrow R^2+\left(Z_{L1}-Z_{L2}\right)^2=5R^2\)

\(\Rightarrow\left|Z_{L1}-Z_{L2}\right|=2R\)

\(\Rightarrow L\left(\omega_2-\omega_1\right)=2R\Rightarrow\frac{1}{\pi}.150\pi=2R\Rightarrow R=75\Omega\)

Đáp án B.

Đúng(0)
VT
Van Tran
2 tháng 1 2017

hay

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Yêu cầu VIP