Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phát biểu nào là chính xác
Các kim loại đều:
A. Dẫn điện tốt, có điện trở suất không thay đổi.
B. Dẫn điện tốt, có điện trở suất thay đổi theo nhiệt độ
C. Dẫn điện tốt như nhau, có điêj trở suất thay đổi theo ngiệt độ
D. Dẫn điện tốt, có điện trở suất thay đổi theo nhiệt độ giống nhau.

Tham khảo:
Trong quá trình sử dụng, suất điện động và điện trở trong của nguồn điện có thay đổi và giảm dần thoe thời gian.
Để đo suất điện động và điện trở trong ta cần áp dụng kiến thức định luật Ôm đối với toàn mạch để từ đó thiết kế ra phương án thí nghiệm phù hợp:
Cường độ dòng điện chạy trong mạch điện kín tỉ lệ thuận với suất điện động của nguồn điện và tỉ lệ nghịch với điện trở toàn phần của mạch đó.
\(I=\dfrac{\xi}{R+r}\)

Tham khảo:
Áp dụng biểu thức hiệu điện thế của đoạn mạch chứa nguồn điện và định luật Ohm đối với toàn mạch để xác định suất điện động và điện trở trong của một pin điện hóa.
Sử dụng các đồng hồ đo điện vạn năng để đo các đại lượng trong mạch điện (đo U và I).

a) Không thể sử dụng đồng hồ đo điện đa năng để đo trực tiếp suất điện động của nguồn điện và điện trở trong của nguồn không vì:
Đồng hồ đo điện đa năng chỉ có thể đo được cường độ dòng điện chạy qua nguồn và hiệu điện thế đặt vào hai đầu của đoạn mạch. Nếu để biến trở R hở mạch thì số chỉ của vôn kế V sẽ gần bằng suất điện động E của nguồn. Số chỉ này không đúng bằng giá trị suất điện động E của pin điện hóa mắc trong mạch vì vẫn có một dòng điện rất nhỏ qua vôn kế V.
b) Để xác định suát điện động và điện trở trong cần xác định: Cường độ dòng điện (I) chạy trong mạch và hiệu điện thế (U) đặt ở hai đầu đoạn mạch.
c) Phương án thí nghiệm
- Phương án 1:
+ Thực hiện đo các giá trị U và I tương ứng khi thay đổi R, ta vẽ đồ thị mô tả mối quan hệ đó, tức U = f (I)
U = E – I.(R0 + r)
+ Ta xác định U0 và Im là các điểm mà tại đó đường kéo dài của đồ thị U = f (I) cắt trục tung và trục hoành:
\(U = E - I({R_0} + r) \Rightarrow \left\{ \begin{array}{l}I = 0 \to U = {U_0} = E\\U = 0 \to I = {I_m} = \frac{E}{{{R_0} + r}}\end{array} \right. \Rightarrow E,r\)
- Phương án 2:
+ Từ \(I = {I_A} = \frac{E}{{R + {R_A} + {R_0} + r}} \Rightarrow \frac{1}{I} = \frac{1}{E}\left( {R + {R_A} + {R_0} + r} \right)\)
đặt y = \(\frac{1}{x}\); x = R; b = RA + R0 + r ⇒ y = \(\frac{1}{E}\left( {x + b} \right)\)
+ Căn cứ các giá trị của R và I trong phương án 1, ta tính các giá trị tương ứng của x và y.
+ Vẽ đồ thị y = f (x) biểu diễn gián tiếp mối liên hệ giữa I và R.
+ Xác định tọa độ của xm và y0 là các điểm mà đồ thị trên cắt trục hoành và trục tung.
\(\left\{ \begin{array}{l}y = 0 \to {x_m} = - b = - \left( {{R_A} + {R_0} + r} \right) \to r\\x = 0 \to {y_0} = \frac{b}{E} \to E\end{array} \right.\)

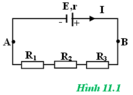
a) Các điện trở hình 11.1 được mắc nối tiếp với nhau nên điện trở tương đương của mạch ngoài là: RN = R1 + R2 + R3 = 5 + 10 + 13 = 18ω
b) Cường độ dòng điện I chạy qua nguồn:
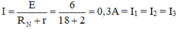
Hiệu điện thế mạch ngoài: UN = I.RN = 18.0,3 = 5,4V
c) Hiệu điện thế giữa hai đầu điện trở R1 là: U1 = R1.I = 5.0,3 = 1,5V