Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

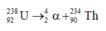
Sau 9 . 10 9 năm thì số gam Urani bị phân rã là:
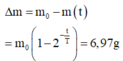
Số mol Urani bị phân rã là :
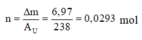
Dựa vào phương trình ta thấy cứ một hạt Urani bị phân rã sẽ tạo thành một hạt Thori suy ra : n Th = n u
Như vậy khối lượng Th tạo thành là :
![]()
Đáp án D

Đáp án D
Chất phóng xạ Urani U 92 235 phóng xạ α tạo thành Thôri (Th)
+Tại một thời điểm nào đó tỉ lệ giữa số nguyên tử Th và nguyên tử U 92 235 bằng 2:
N t h N U = 2
Sau thời gian t số nguyên tử U đã phân rã (cũng chính là số nguyên tử Th tạo ra)
N 1 = N o ( 1 - 2 - 1 T )
Ban đầu (t=0) không có Th, chỉ có U nên 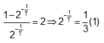
+Sau thời điểm đó ∆ t thì tỉ lệ số nguyên tử nói trên bằng 23
Số nguyên tử U đã phân rã (cũng chính là số nguyên tử Th tạo ra)
N 2 = N o ( 1 - 2 - t + ∆ t T )
Theo đó 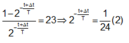
Từ (1) và (2) ta có ∆ t = 3 T = 21 , 9 . 10 8

Khối lượng còn lại của hai đồng vị sau thời gian t là
\(m(238) = m_{0238}.2^{-t/T_1}.\\ m(235) = m_{0235}.2^{-t/T_2}.\)
Chi hai phương trình ta thu được
\(\frac{m(238)}{m(235)} = 2^{t(\frac{1}{T_2}-\frac{1}{T_1})}.(2)\)
mà hiện tại tỉ số khối lượng của chúng là \(\frac{92,848}{7,142} = 13.\)
Thay vào phương trình (2) ta được \(2^{t(1/T_2-1/T_1)} = 13 => t (1/T_2-1/T_1) = \ln_2{13} => t \approx 3,1.10^9\) năm.
Vậy tuổi Trái Đất cỡ 3,1 tỷ năm.

Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.

Đáp án D
Tại thời điểm đề bài cho, gọi số nguyên tử Th là NTh và số nguyên tử Urani là NU
Theo đề bài 1 Urani phóng xạ tạo thành 1 Thori.
Sau thời gian t tính từ thời điểm tỉ lệ bằng 2 thì số nguyên tử Urani còn lại: ![]()
Và số nguyên tử Thori tạo ra sau thời gian t tính từ thời điểm tỉ lệ bằng 2 là:

Theo đề bài tỉ lệ giữa số nguyên tử sau thời gian t là 11 => (2) : (1) = 11
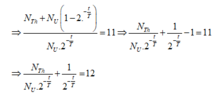
Thay (*) vào phương trình trên ta có:
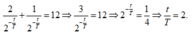
Theo đề T = 7,13.108 (năm) => t = 2.7,13.108 = 14,26.108(năm)

Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
t = 0 Ban đầu t thời điểm cần xác định hiện nay t 1 2
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.

- Khối lượng Urani có trong quặng là:
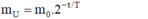
- Khối lượng Chì có trong quặng là:
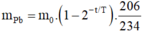
- Suy ra:
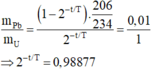
- Tuổi của quặng là: t = 73,33.106 năm.

\(_{92}^{238}U \rightarrow _2^4He + _{90}^{234}\text{Th}\)
Sau 9.109 năm thì số gam Urani bị phân rã là
\(\Delta m = m_0 - m(t) = m_0(1-2^{-t/T}) = 6,97g.\)
Số mol urani bị phân rã là \(n = \frac{\Delta m}{A_{U}} = \frac{6,97}{238} = 0,0293 \text{mol}.\)
Dựa vào phương trình ta thấy cứ 1 hạt Urani bị phân rã sẽ tạo thành 1 hạt Thori. Suy ra \(n_{Th} = n_{urani}\)
Nhưu vậy khối lượng Thori tạo thành là \(m_{Th} = 0,0293.234 = 6,854 g.\)
6,854g