Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Người đó chuyển động theo quỹ đạo đường tròn nên để xác định phương trình quỹ đạo chuyển động của người đó ta cần phải lập phương trình đường tròn.


Cách 1:
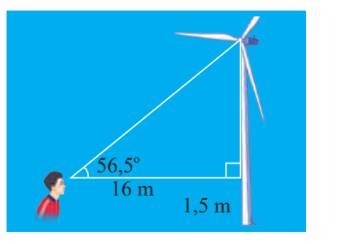
Ta có: \(\widehat B = {90^o} - 56,{5^o} = 33,{5^o}\)
Áp dụng định lí sin, ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow BC = \sin A.\frac{{AC}}{{\sin B}} = \sin 56,{5^o}.\frac{{16}}{{\sin 33,{5^o}}} \approx 24,2\;(m)\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)
Cách 2:
\(\tan A = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\tan A = 16.\tan 56,{5^o} \approx 24,2\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)

không hiểu nổi tại sao lại là 2 lần đường.
XA XB A B C : Lần gặp 1 c: lần gặp 2 xe XA còn qua đoạn CA nữa mới đủ 2 lần xe XB còn qua đoạn CB nữa mới đủ 2 lần tính đến lúc gặp nhau lần 2
Xin lỗi, vì khi cái này đăng lên, câu hỏi trên sẽ bị loại khỏi danh sách "chưa trả lời"

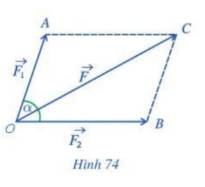
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}
{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\
\begin{array}{l}
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha
\end{array}\\
{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }
\end{array}\)

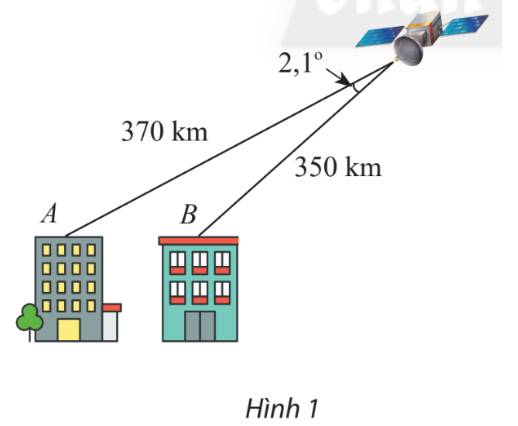
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}\)
Vậy khoảng cách giữa hai tòa nhà là 23,96 km.