Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

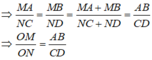

Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
S A E O = S B F O (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
S D E O = S C F O (2)
Từ (1) và (2) suy ra : S O A D = S O B C (3)
Suy ra: OH.AD = OK.BC
⇔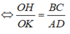

a;Vì AB//CD nên theo định lí Ta-lét ta có:
OA/OC=OB/ODOAOC=OBOD
⇒OA.OD=OC.OB⇒OA.OD=OC.OB
b;Xét ΔAOHΔAOH và ΔCOKΔCOKcó:
AHOˆ=CKO=90oˆAHO^=CKO=90o^
AOHˆ=COKˆAOH^=COK^ (hai góc đối đỉnh)
⇒ΔAOH ΔCOK(g.g)⇒ΔAOH ΔCOK(g.g)
⇒OAOC=OHOK(1)⇒OAOC=OHOK(1)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
ABCD=OAOC(2)ABCD=OAOC(2)
Từ 1 và 2 ta có:
OHOK=ABCD


a) ABCD là hình thang nên AB//CD
CD=2AB ==>AB/CD=1/2
AB//CD, áp dụng định lý Ta-let, ta có
OA/OC=OB/OD=AB/CD=1/2
=>OA/OC=1/2 => OC=2OA
B) Ta có : OA/OC=OB/OD=AB/CD=1/2
==> OD/OB = 2 ==>OD = 2OB
*xét: OC/AC = 2OA/(OA + OC) = 2OA/(OA + 2OA) = 2OA/3OA = 2/3(1);
OD/BD = 2OB/(OD + OB) = 2OB/(2OB + OB) = 2/3(2)
*từ (1),(2) =>OC/AC = OD/BD = 2/3
=>O là trọng tâm tam giác FCD
c)
Vì một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD,AC và BC tại M, I,K và N nên KN//AB ,IM//AB và IN//AB
MI//AB, áp dụng hệ quả của định lý Ta-let, ta có
MI/AB = DM/AD = DI/IB (1)
IN//AB, áp dụng định lý Ta-let, ta có
CN/BC=DI/IB (2)
Từ (1) và (2), ta có
DM/AD=CN/BC
d)
KN//AB, áp dụng hệ quả của định lý Ta-let, ta có
KN/AB=CN/BC
Ta có :KN/AB=CN/BC và MI/AB=DM/AD
mà DM/AD=CN/BC nên KN/AB=MI/AB => KN=MI

1 1 1 1 A H B D K C O
a, Xét 2 tam giác : AOB và COD
\(\widehat{A_1}=\widehat{C_1}\)( 2 góc so le trong )
\(\widehat{B_1}=\widehat{D_1}\)( 2 góc so le trong )
\(\Rightarrow\Delta AOB~\Delta COD\left(gg\right)\)
\(\Rightarrow\frac{AO}{OC}=\frac{OB}{OD}\)
\(\Rightarrow AO.OD=OC.OB\)
b, \(\Delta AOB~\Delta COD\Rightarrow\frac{OA}{OC}=\frac{AB}{CD}\left(1\right)\)
\(\Delta AOH\)và \(\Delta COK\)có :
\(\Rightarrow\frac{OH}{OK}=\frac{AO}{OC}\left(2\right)\)
Từ (1)(2) => \(\frac{OH}{OK}=\frac{AB}{CD}\)

Bài 1:
A B C M N O
Ta có BM là đường trung tuyến
⇒ \(\dfrac{OM}{OB}=\dfrac{1}{2}\)
CN là đường trung tuyến
⇒ \(\dfrac{ON}{OC}=\dfrac{1}{2}\)
Suy ra: \(\dfrac{OM}{OB}=\dfrac{ON}{OC}\Rightarrow OM.OC=ON.OB\)
