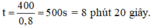Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta gọi vận tốc hai người lần lượt là v1 và v2 (giả sử v2>v1)
khi họ chạy ngược chiều ta có
\(v_1+v_2=\frac{400}{80}=5\) (1)
khi họ chạy cùng chiều muốn gặp nhau tức là người có v2 ấy sẽ phải chạy 1 vòng và 1 đoạn nx để đuổi kịp người v1 ấy ( bạn tưởng tượng là ngay khi người v2 quay lại khoảng cách hai người là C=400(m)
ta có pt : \(400+v_1t_2=v_2t_2\)
\(\Leftrightarrow\left(v_2-v_1\right)=\frac{400}{t_2}=\frac{400}{400}=1\) (2)
từ (1) và (2) ta đc
\(\left\{{}\begin{matrix}v_1=2\left(m/s\right)\\v_2=3\left(m/s\right)\end{matrix}\right.\)

Tóm tắt
\(S_{AB}=10km\)
\(V_1=54km\)/\(h\)
\(V_2=48km\)/\(h\)
____________
\(a\)) \(t=?\)
\(b\)) \(S_{AC}=?\)
Giải
a) 
Gọi \(t_1;t_2\) lần lượt là thời gian đi của người đi vận tốc 54 km/h và 48 km/h.
Ta có:
\(S_{AC}-S_{BC}=S_{AB}=10\Rightarrow V_1.t_1-V_2.t_2=10\)
Trong đó: \(t_1=t_2=t;V_1=54km\)/\(h;V_2=48km\)/\(h\).
\(\Rightarrow10=54.t-48t=t\left(54-48\right)=6t\Rightarrow t=\frac{10}{6}=\frac{5}{3}\left(h\right)\)
b) \(\Rightarrow S_{AC}=54.\frac{5}{3}=90\left(km\right)\)
Vậy nơi 2 người gặp nhau cách điểm A là 90 km

Đổi 2 giờ 30 phút = 2,5 giờ; 30 phút = 0,5 giờ
Hiệu vận tốc là :
50 : 2,5 = 20 (km/giờ)
Tổng vận tốc là :
50 : 0,5 = 100 (km/giờ)
Vận tốc v1 là :
(100 - 20) : 2 = 40 (km/giờ)
Vận tốc v2 là :
100 - 40 = 60 (km/giờ)

Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Sau khoảng thời gian t (s), quãng đường em thứ nhất chạy hơn em thứ hai là:
S = 0,8.t
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quảng đường em thứ nhất chạy hơn em thứ hai trong khoảng thời gian đó bằng đúng chu vi một vòng chạy.
Khi đó ta có: S = 0,8.t = Cchu vi = 400 m
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là: