Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(v^2-v_0^2=2as\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2s}=\dfrac{0^2-10^2}{2\cdot50}=-1\left(m/s^2\right)\)
Quãng đường mà vật di chuyển trong 4s kể từ lúc hãm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2\)
\(\Rightarrow s=10\cdot4+\dfrac{1}{2}\cdot-1\cdot4^2=32\left(m\right)\)

Đáp án C.
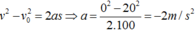
( Dấu - chứng tỏ a → ngược chiều với v → là chiều chuyển động và cũng là chiều dương của ).
- Vận tốc là một đại lượng véctơ nên giá trị của nó(trong một hệ tọa độ) có thể dương, âm hoặc bằng 0. Giá trị dương cho biết vật chuyển động theo chiều dương và ngược lại, giá trị âm cho biết vật chuyển động theo chiều âm của trục tọa độ.
- Tốc độ là đại lượng không âm, tốc độ tức thời là độ lớn của vận tốc tức thời

Vật chuyển động chậm dần đều: \(a=-0,2\)m/s2
\(v_0=54\)km/h\(=15\)m/s
a) Vận tốc của xe sau 20s chuyển động:
\(v=v_0+at=15-0,2\cdot20=11\)m/s
b) Quãng đường xe đi từ lúc hãm phanh đến khi dừng hẳn(v'=0m/s) là:
\(v'^2-v^2_0=2aS\Rightarrow0-15^2=2\cdot\left(-0,2\right)\cdot S\)
\(\Rightarrow S=562,5m\)
Chọn gốc tọa độ tại vị trí xe hãm phanh.
Chiều \(\left(+\right)\) là chiều chuyển động \(\left(v\ge0\right)\).
Gốc thời gian là thời điểm xe hãm phanh.
Lúc \(t=0\) thì \(v_0=72km/h=20m/s\)
\(t=10s\) thì \(v=0\)
\(a,a=?m/s^2\)
Ta có : \(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{10}=\dfrac{0-20}{10}=-2m/s^2\)
\(b,s=?m\)
Ta có : \(d=v_0t+\dfrac{1}{2}at^2=20.10+\dfrac{1}{2}\left(-2\right).10^2=100\left(m\right)\)
Do \(v\ge0\Rightarrow s=d=100m\)
\(c,\) Quãng đường đi được của xe trong 8s đầu là :
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=20.8+\dfrac{1}{2}\left(-2\right).8^2=96\left(m\right)\)
Quãng đường đi được của xe trong 2s cuối là : \(s-s_1=100-96=4\left(m\right)\)
Vì quãng đường trong 2s đầu và 2s cuối có cùng thời gian nên ta có s của 2s đầu và cuối bằng nhau.
Vậy ...