
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)

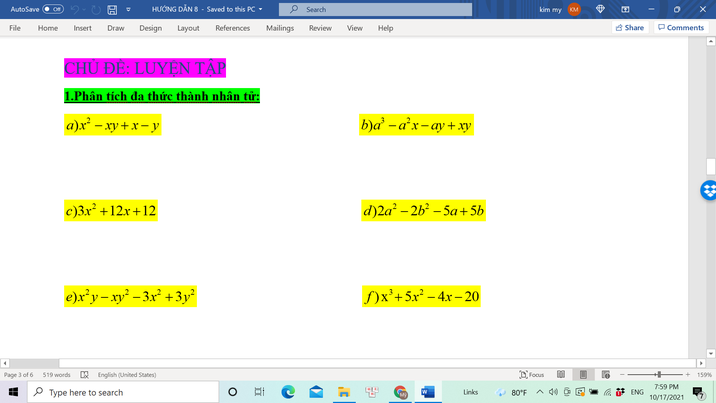
a) \(=x\left(x-y\right)+\left(x-y\right)=\left(x-y\right)\left(x+1\right)\)
b) \(=a^2\left(a-x\right)-y\left(a-x\right)=\left(a-x\right)\left(a^2-y\right)\)
c) \(=3\left(x^2+4x+4\right)=3\left(x+2\right)^2\)
d) \(=2\left(a^2-b^2\right)-5\left(a-b\right)=2\left(a-b\right)\left(a+b\right)-5\left(a-b\right)\)
\(=\left(a-b\right)\left(2a+2b+5\right)\)
e) \(=xy\left(x-y\right)-3\left(x^2-y^2\right)=xy\left(x-y\right)-3\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(xy-3x-3y\right)\)
f) \(=x^2\left(x+5\right)-4\left(x+5\right)=\left(x+5\right)\left(x^2-4\right)\)
\(=\left(x+5\right)\left(x-2\right)\left(x+2\right)\)

\(3x\left(x-y\right)+x-y\)
\(=3x\left(x-y\right)+1\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+1\right)\)



a,\(x^2-7x+6=x^2-x-6x+6\)
\(=x\left(x-1\right)-6\left(x-1\right)\)
\(=\left(x-6\right)\left(x-1\right)\)
a) x2-7x+6=(x2-x)-(6x-6)=x(x-1)-6(x-1)=(x-6)(x-1)
b) x2-6x+3=(x2-6x+9)-6=(x-3)2-\(\sqrt{6^2}\)=(x-3-\(\sqrt{6}\))(x-3+\(\sqrt{6}\))
c) x2-4x+3=(x2-x)-(3x-3)=x(x-1)-3(x-1)=(x-3)(x-1)
d) 3x2-5x+2=(3x2-3x)-(2x-2)=3x(x-1)-2(x-1)=(3x-2)(x-1)
e) 7x2-x-6=(7x2-7x)+(6x-6)=7x(x-1)+6(x-1)=(7x+6)(x-1)
f) 3x2-5x-8=(3x2+3x)-(8x+8)=3x(x+1)-8(x+1)=(3x-8)(x+1)
g) x2-6x+5=(x2-x)-(5x-5)=x(x-1)-5(x-1)=(x-5)(x-1)
h) x2-2x-3=(x2-2x+1)-4=(x-1)2-22=(x-1-2)(x-1+2)=(x-3)(x+1)
i) x2-x-12=(x2+3x)-(4x+12)=x(x+3)-4(x+3)=(x-4)(x+3)


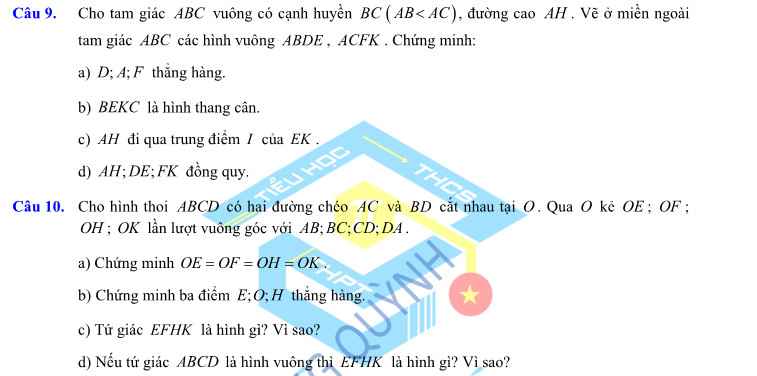
a: Xét ΔABC vuông tại B và ΔABE vuông tại B có
AB chung
BC=BE
=>ΔABC=ΔABE
=>góc EAB=góc CAB
=>AB là phân giác của góc EAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
c: ΔAMH=ΔANH
=>HM=HN
mà HN<HC
nên HM<HC
e: Xét ΔAEC có
AB,CM là đường cao
AB cắt CM tại H
=>H là trực tâm
=>EH vuông góc AC
mà HN vuông góc AC
nên E,H,N thẳng hàng

Bài 8
a, \(A=a^2+b^2=\left(a+b\right)^2-2ab\Rightarrow S^2-2P\)
b, \(B=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\)
\(\Rightarrow S\left(S^2-3P\right)=S^3-3PS\)
c, \(C=a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=\left[\left(a+b\right)^2-2ab\right]^2-2\left(ab\right)^2\)
\(\Rightarrow\left(S^2-2P\right)^2-2P^2\)

Bài 1:
b: \(\Leftrightarrow x^2-2x+4+x^3+8=12\)
\(\Leftrightarrow x^3+x^2-2x=0\)
=>x(x+1)=0
=>x=0 hoặc x=-1
f: \(\Leftrightarrow x+3-6x+12=-5\)
=>-5x=-20
hay x=4(nhận)



 AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ
AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ 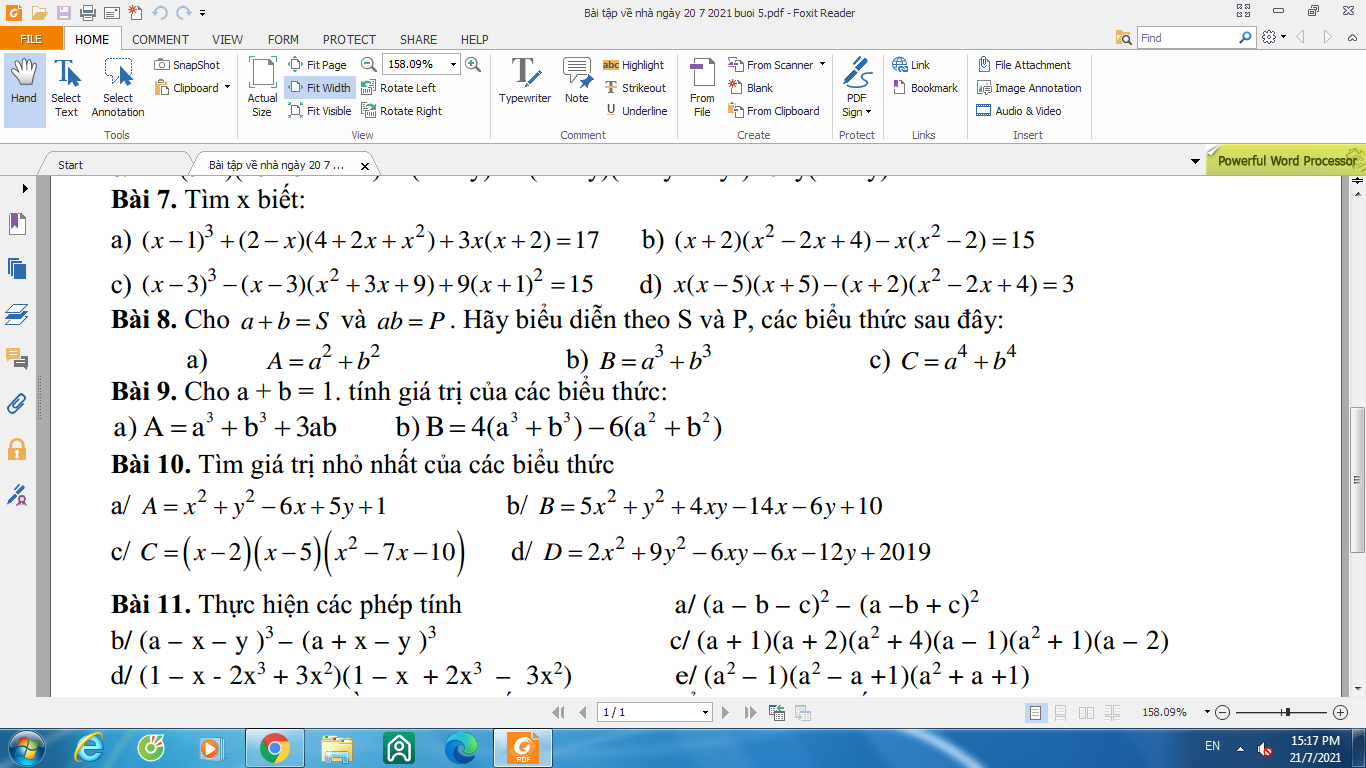

Trả lời:
Bài 1:
a, \(4x^2-10x+7\)
\(=4x^2-10x+\frac{25}{2}+\frac{3}{4}\)
\(=\left(4x^2-10x+\frac{25}{2}\right)+\frac{3}{4}\)
\(=\left[\left(2x\right)^2-2.2x.\frac{5}{2}+\left(\frac{5}{2}\right)^2\right]+\frac{3}{4}\)
\(=\left(2x-\frac{5}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
Vậy đpcm
b, \(2x-4x^2-1\)
\(=-\left(4x^2-2x+1\right)\)
\(=-\left[4x^2-2x+\frac{1}{4}+\frac{3}{4}\right]\)
\(=-\left[\left(2x\right)^2-2.2x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}\right]\)
\(=-\left[\left(2x-\frac{1}{2}\right)^2+\frac{3}{4}\right]\)
\(=-\left(2x-\frac{1}{2}\right)^2-\frac{3}{4}\le-\frac{3}{4}< 0\forall x\)
Vậy đpcm
c, \(4x^2+6x+13\)
\(=4x^2+6x+\frac{9}{4}+\frac{43}{4}\)
\(=\left(4x^2+6x+\frac{9}{4}\right)+\frac{43}{4}\)
\(=\left[\left(2x\right)^2+2.2x.\frac{3}{2}+\left(\frac{3}{2}\right)^2\right]+\frac{43}{4}\)
\(=\left(2x+\frac{3}{2}\right)^2+\frac{43}{4}\ge\frac{43}{4}\forall x\)
Dấu "=" xảy ra khi \(2x+\frac{3}{2}=0\Leftrightarrow x=-\frac{3}{4}\)
Vậy GTNN của bt bằng 43/4 khi x = - 3/4
d, \(-8x-x^2+3\)
\(=-\left(x^2+8x-3\right)\)
\(=-\left(x^2+8x+16-19\right)\)
\(=-\left[\left(x+4\right)^2-19\right]\)
\(=-\left(x+4\right)^2+19\le19\forall x\)
Dấu "=" xảy ra khi x + 4 = 0 <=> x = - 4
Vậy GTLN của bt bằng 19 khi x = - 4
Trả lời:
Bài 2:
a, \(3x^3-18x^2+27x=0\)
\(\Leftrightarrow3x\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow3x\left(x-3\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x=0\\\left(x-3\right)^2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=3\end{cases}}}\)
Vậy x = 0; x = 3 là nghiệm của pt.
b, \(6x\left(x-3\right)=x^3-9x\)
\(\Leftrightarrow6x\left(x-3\right)-\left(x^3-9x\right)=0\)
\(\Leftrightarrow6x\left(x-3\right)-x\left(x^2-9\right)=0\)
\(\Leftrightarrow6x\left(x-3\right)-x\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left[6x-x\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(6x-x^2-3x\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-x^2+3x\right)=0\)
\(\Leftrightarrow x\left(x-3\right)\left(3-x\right)=0\)
\(\Leftrightarrow-x\left(x-3\right)\left(x-3\right)=0\)
\(\Leftrightarrow-x\left(x-3\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}-x=0\\\left(x-3\right)^2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=3\end{cases}}}\)
Vậy x = 0; x = 3 là nghiệm của pt.
c, \(4x^3-6x^2+2x=0\)
\(\Leftrightarrow4x\left(x^2-\frac{3}{2}x+\frac{1}{2}\right)=0\)
\(\Leftrightarrow4x\left(x^2-2.x.\frac{3}{4}+\frac{9}{16}-\frac{1}{16}\right)=0\)
\(\Leftrightarrow4x\left[\left(x-\frac{3}{4}\right)^2-\frac{1}{16}\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x=0\\\left(x-\frac{3}{4}\right)^2-\frac{1}{16}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\\left(x-\frac{3}{4}\right)^2=\frac{1}{16}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=0\\x=1;x=\frac{1}{2}\end{cases}}}\)
Vậy x = 0; x = 1; x = 1/2 là nghiệm của pt.