Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E M N I
Haizzz học lâu quá nên quên hết rồi ! sorry

a) Chứng minh D E A ^ = 180 0
b) Chứng minh
A I M ^ = A K M ^ = I A K ^ = 90 0
c) Chứng minh DDME có E D M ^ = D E M ^ = 45 0
Þ DDME vuông cân ở M.

Bài 1:
A B C D M N P Q E F
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)
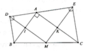
A B C M D E F K
a) Các tam giác DBA và tam giác EAC vuông cân nên \(\widehat{ABD}=\widehat{DAB}=45^o,\widehat{CAE}=\widehat{ECA}=45^o\).
\(\widehat{DAE}=\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=45^o+90^o+45^o=180^o\).
Suy ra D, A, E thẳng hàng.
b) Có M là trung điểm của BC và tam giác BAC vuông tại A nên MA = MB = MC.
Suy ra \(\Delta DBM=\Delta DAM\left(c.c.c\right)\). Vì vậy \(\widehat{BDM}=\widehat{ADM}\) hay DM là tia phân giác góc ADB.
mà tam giác BDA cân tại D nên DM cũng là đường cao hay \(DM\perp AB\).
Tương tự cho \(EM\perp AC\).
c) Theo chứng minh trên DM là tia phân giá góc ADB nên \(\widehat{BDM}=\widehat{MDA}=45^o\). Tương tự \(\widehat{AEK}=\widehat{KEC}=45^o\).
Vì vậy ta, giác DME vuông cân.
d) Do các tam giác ADB và tam giác AEC cân và DF và EK là đường cao tương ứng nên DF và EK cũng là các đường trung tuyến.
Vì vậy F và K lần lượt là trung điểm của AB và AC.
Từ đó suy ra FK là đường trung bình của tam giác BAC hay \(FK=\frac{1}{2}BC\).
tại sao ma=mb=mc