Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Do A thuộc đường trung trực của DH nên:
=> AD = AH (theo t/ch đường trung trực)
Do A thuộc đường trung trực của HE nên:
=> AH = AE (theo t/ch đường trung trực)
Mà AH = AD (cmt) nên:
=> AD = AE
=> tam giác ADE cân tại A (đpcm)
Mấy câu sau mk sẽ giải cho nha bn! Giờ mk đg dùng máy điện thoại!
Chúc bn hok tốt???

a)Nối AD,AE.Ta có :
AD = AH vì nằm trên đường trung tuyến của DH
AE = AH vì nằm trên đường trung tuyến của EH
=> AD = AE hay tam giác ADE cân
Xét \(\Delta ADB\)và \(\Delta AHB\)
+ AB chung
+ AD = AH
+\(\widehat{DAB}=\widehat{HAB}\)
\(\Rightarrow\Delta ADB=\Delta AHB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADB}=\widehat{AHB}=90^0\)
Chứng minh tương tự ta được tam giác AEC vuông tại E
Suy ra \(90^0-\widehat{ADE}=90^0-\widehat{AED}\Leftrightarrow\widehat{IDB}=\widehat{KEC}\)
Mà \(\widehat{IDB}=\widehat{IHB};\widehat{KEC}=\widehat{KHC}\)
\(\Rightarrow\widehat{IHB}=\widehat{KHC}\)
Kéo dài IH về phía H.Lấy điểm S bất kì thuộc tia đối của IH
Xét tam giác IKH có KC là tia phân giác của góc ngoài HKE và HC là tia phân giác góc ngoài KHS
Chứng minh HC là phân giác của góc KHS
Ta có \(\widehat{IHB}=\widehat{CHS}=\widehat{KHC}\)(đối đỉnh)
\(\Rightarrow\widehat{KHC}=\widehat{CHS}\)
Vậy hai tia phân giác của hai góc ngoài của tam giác IKH cắt nhau tại .Suy ra IC là tia phân giác của góc KIH
b) Ta có IB là phân giác của góc DIH
IC là phân giác của góc HIK
Mà hai góc trên kề bù
=> IB và IC vuông góc với nhau
(Hình bạn lên mạng tra theo đề là ra nhiều lắm nhé mình ko biết vẽ hình trên OLM bạn thông cảm)

UhkbijhihguhftfWegvhhhhvhiggyghkbhijmkjiphfuhfygggubh

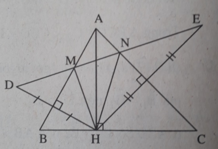
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của ΔHMN.
Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác trong của góc MHN của ΔHMN.
+) HC vuông góc với HA tại H mà HA là đường phân giác trong của góc MHN nên HC là đường phân giác góc ngoài của ΔHMN.( đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)
+) Các đường thẳng HC và NC cắt nhau tại C; HC và NC là hai đường phân giác ngoài của tam giác HMN nên MC là đường phân giác góc trong của ΔHMN.
MB và MC là các tia phân giác của hai góc kề bù ∠DMH; ∠HMA nên MB ⊥ MC.
Vậy MC ⊥ AB.

cách này của lớp 8 nhé:
tự chứng minh BAC=1/2DAE
Mà MHB=1/2DAE
=> BAC=MHB
mà góc B chung của 2 tam giác BAC và MHB
=> tam giác BAC đồng dạng tam giác BHM (g.g)
=> \(\frac{AB}{BH}=\frac{BC}{BM}\Rightarrow\frac{AB}{BC}=\frac{BH}{BM}\)
Mà góc B chung của tam giác BHA và BMC
=> tam giác BHA đồng dạng tam giác BMC
=> BHA=BMC=90 độ => CM vuông góc AB
chứng minh tương tự => BN v góc
cách 2 (lớp 9)
giống như cách trên ta chứng minh được MHB=BAC
hay MHB=MAC
=> MAC+MHC=180
=> tứ giác AMHC nội tiếp
=> AMC=AHC=90
=> CM vuông góc AB