Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F
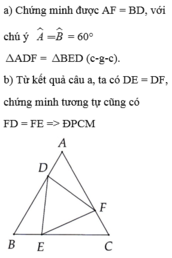
Ta có AB = BC = CA, AD = BE = CF
nên AB - AD = BC - BE = CA - CF hay BD = CE = AF.
\(\Delta ABC\) đều \(\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
Xét hai tam giác ADF và BED có:
BD = AF (cmt)
\(\widehat{A}=\widehat{B}\left(cmt\right)\)
BE = AD (gt)
Vậy: \(\Delta ADF=\Delta BED\left(c-g-c\right)\)
\(\Rightarrow\) DF = DE (hai cạnh tương ứng)
Xét hai tam giác EBD và FCE có:
BD = CE (cmt)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
BE = CF (gt)
Vậy: \(\Delta EBD=\Delta FCE\left(c-g-c\right)\)
\(\Rightarrow\) DE = EF (hai cạnh tương ứng)
Do đó DF = DE = EF. Vậy \(\Delta DEF\) là tam giác đều.

AB=AC=BC
AD=BE=CF
=>BD=EC=AF
Xet ΔADF và ΔBED có
AD=BE
góc A=góc B
AF=BD
=>ΔADF=ΔBED
=>DF=ED
Xét ΔADF và ΔCFE có
AD=CF
góc A=góc C
AF=CE
=>ΔADF=ΔCFE
=>DF=FE=ED
=>ΔDEF đều

đăg lên hoc24.vn đi
ko thì bn vẽ hình ra mk xem thử ha
Mik cho pn mấy cách làm nha !
C1 : CM 3 cạnh của tam giác bằng nhau
C2 : CM 3 góc của tam giác bằng nhau
C3 : CM tam giác cân tại 2 đỉnh
C4 : CM tam giác cân có 1 góc bằng 60 °
➡ Pn dựa vào đó làm nha ! Hay thì cho mik cái tich

A B C D E F
(Mình sửa lại đề nha bạn)
Cho \(\Delta\) ABC đều. Lấy các điểm D, E, F theo thứ tự thuộc AB, BC, CA sao cho AD = BE = CF. Chứng minh \(\Delta\) DEF đều.
\(\Delta\) ABC đều (gt) \(\Rightarrow\) AB = BC = AC
và \(\widehat{A}\) = \(\widehat{B}\) = \(\widehat{C}\) = 60o
mà AD = BE = CF (gt)
\(\Rightarrow\) AB - AD = BC - BE = AC - CF
\(\Rightarrow\) BD = CE = AF
Xét \(\Delta\) ADF và \(\Delta\) EBD, có:
AD = BE (gt)
\(\widehat{DAF}\) = \(\widehat{EBD}\) = 60o (cmt)
AF = BD (cmt)
\(\Rightarrow\) \(\Delta\)ADF = \(\Delta\) EBD (c.g.c)
\(\Rightarrow\) DF = ED (2 cạnh tương ứng) (1)
Xét \(\Delta\) ADF và \(\Delta\) CFE, có:
AD = CF (gt)
\(\widehat{DAF}\) = \(\widehat{FCE}\) = 60o (cmt)
AF = CE (cmt)
\(\Rightarrow\) \(\Delta\) ADF = \(\Delta\) CFE (c.g.c)
\(\Rightarrow\) DF = FE (2 cạnh tương ứng) (2)
Từ (1) và (2) \(\Rightarrow\) DF = FE = ED
Vậy \(\Delta\) DEF đều
_Yorin_

Tự vẽ hình.
Vì \(\Delta ABC\) đều nên AB = AC = BC
và \(\widehat{ABC}=\widehat{ACB}=\widehat{BAC}\)
hay \(\widehat{DBE}=\widehat{FCE}=\widehat{DAF}\)
mà AD = CF = BE
=> AB \(-\) AD = AC \(-\) CF = BC \(-\) BE
=> BD = AF = CE
Xét \(\Delta\)ADF và \(\Delta\)BED có:
AD = BE (gt)
\(\widehat{DAF}\) = \(\widehat{EBD}\) (c/m trên)
AF = BD (c/m trên)
=> \(\Delta\)ADF = \(\Delta BED\) (c.g.c)
=> DF = ED (2 cạnh t/ư) (1)
Xét \(\Delta\)ADF và \(\Delta\)CFE có:
AD = CF (gt)
\(\widehat{DAF}\) = \(\widehat{FCE}\) (c/m trên)
AF = CE (c/m trên)
=> \(\Delta ADF\) = \(\Delta CFE\left(c.g.c\right)\)
=> DF = FE (2 cạnh t/ư) (2)
Từ (1) và (2) suy ra DF = ED = FE
Do đó \(\Delta\)DEF đều.

A B C D E F
\(\Delta ABC\)đều (gt) nên AB = BC = AC ; góc A = góc B = góc C = 600 mà AD = BE = CF (gt)
=> AB - AD = BC - BE = AC - CF <=> BD = CE = AF
\(\Delta ADF,\Delta BED\)có AD = BE (gt) ; góc DAF = góc EBD = 600 (cmt) ; AF = BD (cmt) nên\(\Delta ADF=\Delta BED\left(c.g.c\right)\)
=> DF = ED (2 cạnh tương ứng) (1)
\(\Delta ADF,\Delta CFE\)có AD = CF (gt) ; góc DAF = góc FCE = 600 (cmt) ; AF = CE (cmt) nên\(\Delta ADF=\Delta CFE\left(c.g.c\right)\)
=> DF = FE (2 cạnh tương ứng) (2).Từ (1) và (2),ta có DF = FE = ED.Vậy\(\Delta DEF\)đều

Hình tự vẽ
Xét 3 tam giác \(ADF,BED,CFE\),ta có:
\(AD=BE=CF\)(gt )
\(\widehat{A}=\widehat{B}=\widehat{C}\)(gt)
DB=EC=AD ( do các cạnh của tam giác đều ABC - các cạnh AD,BE,FC = nhau )
=>3 tam giác \(ADF,BED,CFE\)=nhau
=> DE=DF=FE
=> tam giác DEF đều
P/s tham khảo nha
A B C D E F
Ta có: AB=BC=CA (t/g ABC đều)
AD=BE=CF
=>BD=CE=AF
Xét t/g ADF và t/g BED có:
AD=BE (gt)
góc A=góc B = 60 độ (gt)
AF=BD (cmt)
=>t/g ADF = t/g BED (c.g.c)
=>DF = DE (1)
Xét t/g ADF và t/g CFE có:
AD = CF (gt)
góc A=góc C = 60 độ (gt)
AF = CE (cmt)
=>t/g ADF = t/g CFE (c.g.c)
=> DF = EF (2)
Từ (1) và (2) => DF = DE = EF => t/g DEF đều

A B C E F D
hình chỉ minh họa thôi nhé mk sẽ giải cho
vì AD=BE=CF nên AD,BE,CF là đường cao là trung trực là tung tuyến phân giác mà 3 đường cao đi qua 1 điểm , điểm này cách đều D,E,F nên tam giác DEF là tam giac đều
b)
(x-5)(y+1)=7
=>\(\hept{\begin{cases}x-5=1\\y+1=7\end{cases}}\)hoặc \(\hept{\begin{cases}x-5=-1\\y+1=-7\end{cases}}\)
=>\(\hept{\begin{cases}x=6\\y=6\end{cases}}\) hoặc \(\hept{\begin{cases}y=4\\y=-2\end{cases}}\)