Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H (lm theo cảm giác nghĩ là ko đúng :3333
ta thấy rằng ab bằng với ac nên cạnh ab cũng có là 15cm
vì đây là tam giác cân nên đoạn độ dài đáy có được chia ra làm hai nửa đều nhau nên cạnh HC cũng ;là 5m
hm hình như mik vẽ hình sai phải không hay lm sai

TA CÓ TAM GIÁC ABH VUÔNG TẠI H ;A/D ĐỊNH LÝ PYTAGO TA CÓ
\(AB^2=AH^2+BH^2=>BH^2=AB^2-AH^2\)
=>\(BH^2=15^2-12^2=>BH^2=81=>BH=9'\left(cm\right)\)
=>\(BC=9+16=25\left(cm\right)\)
ta có \(\Delta AHC\) VUÔNG TẠI H A/D ĐỊNHLÝ PYTAGO TA CÓ
\(AC^2=AH^2+HC^2=>AC^2=12^2+16^2\)
=>\(AC^2=400=>AC=20\left(cm\right)\)

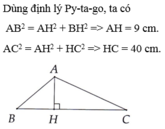
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)

a, Ta có ∆ABC cân ở A(gt)
AH\(\perp\) BC=>AH là đường cao
(1)=>AH đồng thời là trung tuyến=>HB=HC
(2)=>AH đồng thời là phân giác=>góc BAH=góc CAH
b, Áp dụng định lí pyta go cho ∆ABH ta có
AB2=AH2+BH2 =>52=42+HB2=>HB=√52--42=3
d, Xét ∆DHB và ∆EHC có
Góc HDB=góc HEC =90°(HD\(\perp\) AB, HE vuông góc ACgt)
Góc B=góc C ( tam giác ABC cân tai A gt)
HB =HC (cmt)
=> ∆DHB=∆EHC(ch-cgv)=>HD=HE=>∆HDE cân tại H
Xét \(\Delta ABH\) vuông tại H có :
\(AB^2=AH^2+BH^2=12^2+5^2=169\Rightarrow AB=13cm\)
Xét \(\Delta ACH\) vuông tại H có :
\(AC^2=AH^2+HC^2\Rightarrow HC^2=AC^2-AH^2=15^2-12^2=81\Rightarrow HC=9\)
Vậy ...
\(AH^2=BH.CH\Rightarrow12^2=5.CH\Rightarrow CH\approx28cm\)
\(BC=BH+CH=5+28=33cm\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{33^2-15^2}\approx29cm\)