Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
c: Ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)
d: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
hay BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{5}{7}\)
Do đó: BD=15/7(cm); CD=20/7(cm)

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
c: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

a, Xét 2 tam giác vuông đó có: (ADB)=(CBD) (cùng phụ với góc BDC)
b, AH.BD=AD.AB vì bằng 2 lần diện tích tam giác ADB.
c, Áp dụng hệ thức lượng trong tam giác vuông tính được AH.
Biết AH, BD tính được S tam giác.

a: Xét ΔHAD vuông tại H và ΔABD vuông tại A có
góc HDA chung
=>ΔHAD đồng dạng với ΔABD
b: ΔABD vuông tại A có AH là đường cao
nên DA^2=DH*DB
c: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
DH=6^2/10=3,6cm

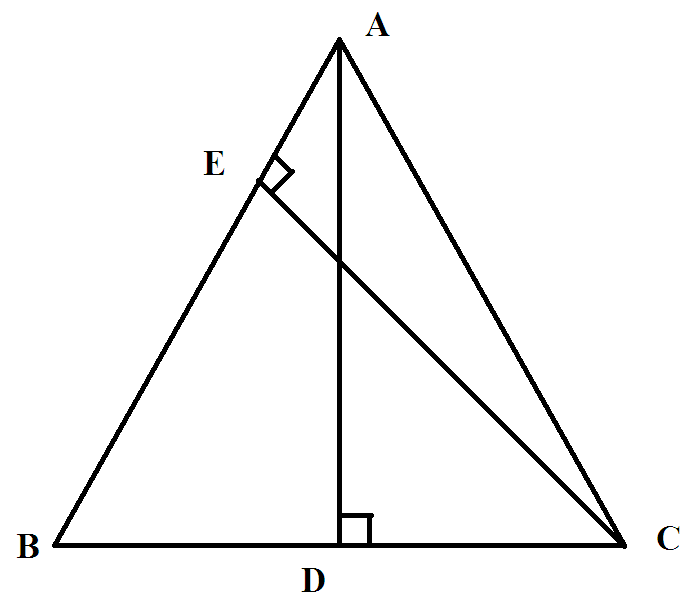
a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)

a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc ABD chung
=>ΔABD đồng dạng với ΔHBA
b: BD=căn 3^2+4^2=5cm
HB=AB^2/BD=3,2cm
c: AD là phân giác
=>ED/EB=AD/AB
mà AD/AB=AH/BH
nên ED/EB=AH/BH