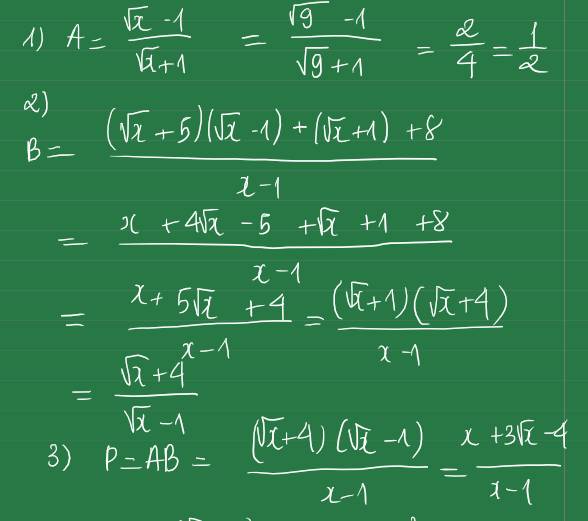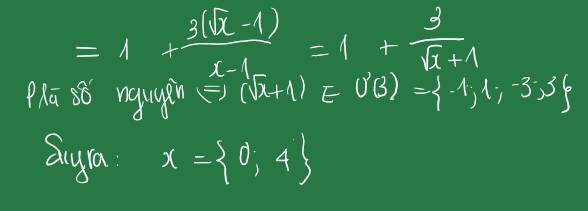Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 :
a)
\(P = a + b - ab = 2 + \sqrt{3} + 2-\sqrt{3} - (2 + \sqrt{3})(2-\sqrt{3})\\ =4 - (2^2 - (\sqrt{3})^2) = 4 - (4 - 3) = 3\)
b)
\(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3x+y=5\\3x-6y=-9\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}y-\left(-6y\right)=5-\left(-9\right)\\x=\dfrac{5-y}{3}\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}y=2\\x=\dfrac{5-2}{3}=1\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình (x ; y) = (1 ; 2)
Câu 1:
a)
\(P=a+b-ab\\ =2+\sqrt{3}+2-\sqrt{3}-\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)\\ =4-\left(4-2\sqrt{3}+2\sqrt{3}-3\right)\\ =4-1=3\)
Vậy \(P=3\)
b)
\(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x+2y=10\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7x=7\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\1-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\2y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy pht có nghiệm là \(\left(x;y\right)=\left(1;2\right)\)

Câu I
1)
a) Ta có: x-5=0
nên x=5
Vậy: S={5}
b) Ta có: \(x^2-4x+3=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Vậy: S={1;3}
2) Ta có: \(\left\{{}\begin{matrix}2x-y=1\\3x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=5\\2x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x-1=2\cdot1-1=1\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(1;1)
II.
1.
\(A=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right].\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)^2}\)
\(=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right).\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}\)
\(=2.\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
2.
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
\(A\in Z\Leftrightarrow\sqrt{x}-1\inƯ_2=\left\{\pm1;\pm2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
\(\Leftrightarrow x\in\left\{0;4;9\right\}\)

Câu 5 :
Ta chứng minh bđt phụ: \(x^5+y^5\ge xy\left(x^3+y^3\right)\forall x\in N\Leftrightarrow x^5+y^5-x^4y-xy^4\ge0\Leftrightarrow\left(x-y\right)x^4-y^4\left(x-y\right)\ge0\Leftrightarrow\left(x-y\right)\left(x^4-y^4\right)\ge0\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\left(x^2+y^2\right)\ge0\)
\(\Rightarrow x^5+y^5\ge xy\left(x^3+y^3\right)\) (1)
\(x^3+y^3\ge xy\left(x+y\right)\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\ge0\Rightarrow x^3+y^3\ge xy\left(x+y\right)\left(2\right)\)
Áp dụng bđt (1) và (2): \(\Rightarrow\dfrac{ab}{a^5+b^5+ab}\le\dfrac{ab}{ab\left(a^3+b^3\right)+ab}\le\dfrac{ab}{a^2b^2\left(a+b\right)+ab}=\dfrac{1}{ab\left(a+b\right)+1}=\dfrac{abc}{ab\left(a+b+c\right)}=\dfrac{c}{a+b+c}\) Tương tự:
\(\dfrac{bc}{b^5+c^5+bc}\le\dfrac{a}{a+b+c};\dfrac{ca}{c^5+a^5+ca}\le\dfrac{b}{a+b+c}\)
\(\Rightarrow\sum\dfrac{ab}{a^5+b^5+ab}\le\sum\dfrac{c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
Dấu = xảy ra \(\Leftrightarrow a=b=c\)=1
Câu 1:
a) Ta có: \(\left(x+3\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)
Vậy: S={1;-7}
b) Ta có: \(\left\{{}\begin{matrix}2x+y-3=0\\\dfrac{x}{4}=\dfrac{y}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=3\\\dfrac{1}{4}x-\dfrac{1}{3}y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+2y=6\\4x-\dfrac{16}{3}y=-16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{22}{3}y=22\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\2x=3-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=3\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(0;3)

hỏi trước tí, bạn biết giải cái hệ này chứ?
\(\left\{{}\begin{matrix}2x+y=3\\2x-3y=1\end{matrix}\right.\)

a, Với \(x>0;x\ne1\)
\(P=\left(\frac{\sqrt{x}}{2}-\frac{1}{2\sqrt{x}}\right)^2\left(\frac{\sqrt{x}-1}{\sqrt{x}+1}-\frac{\sqrt{x}+1}{\sqrt{x}-1}\right)\)
\(=\left(\frac{x-1}{2\sqrt{x}}\right)^2\left(\frac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{x-1}\right)\)
\(=\frac{x^2-2x+1}{4x}.\frac{-4\sqrt{x}}{x-1}=\frac{1-x}{\sqrt{x}}\)
Thay x = 4 => \(\sqrt{x}=2\)vào P ta được :
\(\frac{1-4}{2}=-\frac{3}{2}\)
c, Ta có : \(P< 0\Rightarrow\frac{1-x}{\sqrt{x}}< 0\Rightarrow1-x< 0\)vì \(\sqrt{x}>0\)
\(\Rightarrow-x< -1\Leftrightarrow x>1\)

a: \(=-4+2\sqrt{5}-\sqrt{5}+2+\sqrt{5}=2\sqrt{5}-2\)
b: \(B=\dfrac{2\sqrt{x}+4+6\sqrt{x}-3-2\sqrt{x}}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}}{6\sqrt{x}+4}\)
\(=\dfrac{\left(6\sqrt{x}+1\right)\cdot\sqrt{x}}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)\left(6\sqrt{x}+4\right)}\)

Bài 6:
a: \(\Leftrightarrow\sqrt{x^2+4}=\sqrt{12}\)
=>x^2+4=12
=>x^2=8
=>\(x=\pm2\sqrt{2}\)
b: \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>x+1=1
=>x=0
c: \(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}-20=0\)
=>\(\sqrt{2x}=2\)
=>2x=4
=>x=2
d: \(\Leftrightarrow2\left|x+2\right|=8\)
=>x+2=4 hoặcx+2=-4
=>x=-6 hoặc x=2