Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

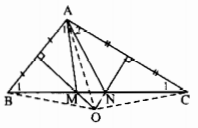
a: Xét ΔAOM và ΔBOM có
OM chung
MA=MB
OA=OB
=>ΔAOM=ΔBOM
Xét ΔAON và ΔCON có
OA=OC
ON chung
NA=NC
=>ΔAON=ΔCON
b: ΔAOM=ΔBOM
=>góc OAM=góc OBM
ΔAON=ΔCON
=>góc OAN=góc OCN
OA=OB
OA=OC
=>OB=OC
=>góc OBN=góc OCM
=>góc OAM=góc OAN
=>AO là phân giác của góc MAN

Theo bài 8.3 ta đã có\(\widehat{A_1} =\widehat{B}_1;\widehat{A_2}=\widehat{C_1} \) (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat{OAB}=\widehat{OBA},\widehat{OAC}=\widehat{OCA},\widehat{OCB}=\widehat{OBC}\)Kết hợp với (1) \(\widehat{OBM}=\widehat{OAM},\widehat{OCN}=\widehat{OAN}\) hay\(\widehat{OAM}=\widehat{OBC}=\widehat{OCB}=\widehat{OAN}\) . Vậy OA là tia phân giác góc MAN.
Hình thì bạn kia vẽ rồi nên mình không vẽ nữa nha
Theo bài 8.3 ta đã cóˆA1=ˆB1;ˆA2=ˆC1A1^=B^1;A2^=C1^ (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ˆOAB=ˆOBA,ˆOAC=ˆOCA,ˆOCB=ˆOBCOAB^=OBA^,OAC^=OCA^,OCB^=OBC^Kết hợp với (1) ˆOBM=ˆOAM,ˆOCN=ˆOANOBM^=OAM^,OCN^=OAN^ hayˆOAM=ˆOBC=ˆOCB=ˆOANOAM^=OBC^=OCB^=OAN^ . Vậy OA là tia phân giác góc MAN.
A B C O N M
a) Ta có: \(\widehat{ABC}=\widehat{ABO}+\widehat{OBM},\widehat{ACB}=\widehat{ACO}+\widehat{OCB}\)
=> \(\widehat{ABC}-\widehat{ACB}=\widehat{ABO}+\widehat{OBC}-\widehat{ACO}-\widehat{OCB}=\left(\widehat{ABO}-\widehat{ACO}\right)+\left(\widehat{OBC}-\widehat{OCB}\right)\)
Mà các đường trung trực của AB, AC cắt nhau tại O
=> O là trực tâm
=> O thuộc đường trung trực của Bc
=> \(\widehat{OBC}=\widehat{OCB}\Rightarrow\widehat{OBC}-\widehat{OCB}=0\)
=> \(\widehat{ABC}-\widehat{ACB}=\widehat{ABO}-\widehat{ACO}\)
Mặt khác O thuộc đường trung trực AB, AC
=> \(\widehat{ABO}=\widehat{BAO},\widehat{OAC}=\widehat{ACO}\)
Vậy nên \(\widehat{ABC}-\widehat{ACB}=\widehat{BAO}-\widehat{CAO}\)(*)
b) Ta có: M thuộc đường trung trực AB
=> \(\widehat{MBA}=\widehat{MAB}=\widehat{MAO}+\widehat{OAB}\)(1)
Tương tự N thuộc đường trung trực AC
=> \(\widehat{NCA}=\widehat{NAO}+\widehat{OAC}\)(2)
Từ (1) , (2) => \(\widehat{ABC}-\widehat{ACB}=\widehat{MBA}-\widehat{NCA}=\left(\widehat{MAO}+\widehat{OAB}\right)-\left(\widehat{NAO}+\widehat{OAC}\right)\)
\(=\left(\widehat{MAO}-\widehat{NAO}\right)+\left(\widehat{OAB}-\widehat{OAC}\right)\)(**)
Từ (*), (**) suy ra \(\widehat{MAO}-\widehat{NAO}=0\Rightarrow\widehat{MAO}=\widehat{NAO}\)
=> AO là phân giác góc MAN
Cảm ơn nha