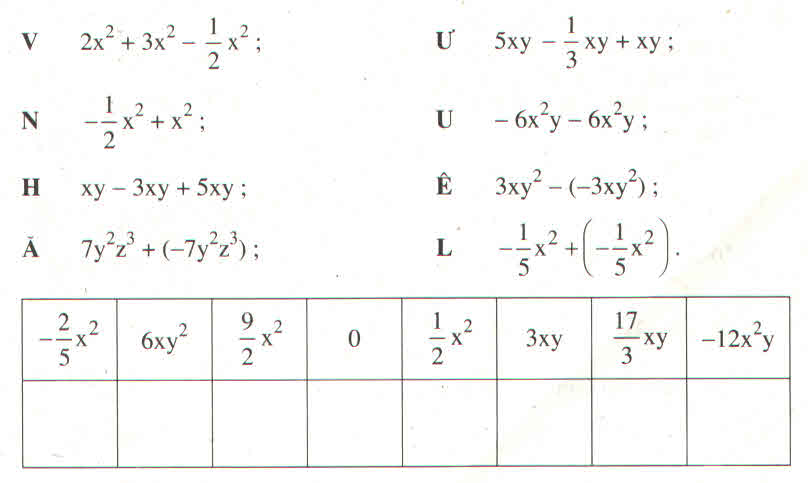K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 4 2017
Hướng dẫn giải:
Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V 2x2 + 3x2 – 1212 x2 = 9292 x2;
Ư 5xy – 1313 xy + xy = 173173 xy;
N - 1212 x2 + x2 = 1212 x2;
U - 6x2y – 6x2y = -12x2y ;
H xy – 3xy + 5xy = 3xy;
Ê 3xy2 – (-3xy2) = 6 xy2;
Ă 7y2z3 + (-7y2z3) = 0;
L - 1515 x2 + (- 1515 x2) = - 2525 x2;

Vậy tên của tác giả cuốn Đại VIệt sử kí là Lê Văn Hưu.
SG
1

19 tháng 4 2017
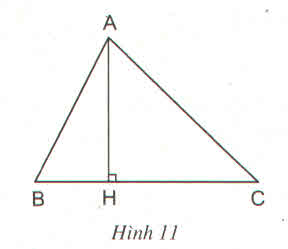
Vì AB < AC (gt) mà AB, AC là hai đường xiên có hai hình chiếu tương ứng là HB và HC nên HB > HC