Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi A D = x 5 ≤ x ≤ 74 . Khi đó thì B D = x 2 − 25 ⇒ C D = 7 − x 2 − 25 .
Tổng thời gian đi từ A đến C là
Đáp án B
Phân tích:
● Ta có thể mô tả bài toán trên bằng hình vẽ sau:
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định
● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
Goi H, K, C, D là các điểm như hình vẽ.
Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
Cách giải: Gọi độ dài đoạn MB là x 
Tam giác ABM vuông tại B => 
Thời gian người đó đi từ A tới C: 
Xét hàm số f(x) 
=> x = 2 5
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5
Theo đề ta có:
Đoạn FE là
FE= 200. 2= 400 (km)
Vận tốc xe thứ 3 là:
50. 2= 100 ( km)
Quang đường xe thứ 3 nhiều hơn xe thứ 2 là;
200 + 10= 210 ( km)
Hiệu của hai vận tốc là:
100- 4= 60 ( km)
Thời gian 2 xe gặp nhau và gấp đôi xe thứ hất là:
210 : 60=3,5 ( giờ)
Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần số giờ là:
7 + 3,5= 10,5 ( giờ)
Đổi 10,5 giờ= 10 giờ 30 phút
Vậy: Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần 10 giờ 30 phút
Đáp án C
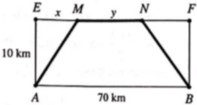
B M = x k m , 0 < x < 25 ta có
A M = A B 2 + B M 2 = x 2 + 100 = x 2 + 100 k m , M C = B C − B M = 25 − x k m
Thời gian bạn A đi xe buýt từ nhà đến điểm hẹnM là t A = x 2 + 100 30 h
Thời gian bạn A, B đi xe máy từ điểm hẹn M đến nhà bạn C là t A B = 25 − x 50 h
Suy ra thời gian bạn A đi từ nhà đến nhà bạn C là t x = t A + t A B = x 2 + 100 30 + 25 − x 50 h
Để bạn A đến nhà bạn C nhanh nhất thì hàm số t(x) đạt giá trị nhỏ nhất, với 0 < x < 25
Ta có t ' x = x 30 x 2 + 100 + 1 50 ; t ' x = 0 ⇔ x = 15 2
Lập bảng biến thiên, ta thấy hàm số t(x) đạt giá trị nhỏ nhất bằng t 15 2 = 23 30 h khi x = 15 2 k m = B M ⇒ M C = 25 − x = 35 2 k m .
Khi đó 5 B M + 3 M C = 5. 15 2 + 3. 35 2 = 90