Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 ở t 0 = 0 ° C ; còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc nhôm và của lượng nước đựng trong cốc ở nhiệt độ t 1 = 20 ° C. Nếu gọi t ° C là nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết thì lượng nhiệt do cục nước đá ở t 0 = 0 ° C đã thu vào để tan thành nước ở t ° C bằng :
Q = λ m 0 + c 2 m 0 (t - t 0 ) = m 0 ( λ + c 2 t)
Còn nhiệt lượng do cốc nhôm và lượng nước đựng trong cốc ở t 1 = 20 ° C. toả ra để nhiệt độ của chúng giảm tới toC (với t < t 1 ) có giá trị bằng :
Q'= ( c 1 m 1 + c 2 m 2 )( t 1 - t)
Theo định luật bảo toàn năng lượng, ta có :
Q' = Q ⇒ ( c 1 m 1 + c 2 m 2 ) ( t 1 - t) = m 0 ( λ + c 2 t)
Từ đó suy ra :
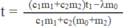
Thay số : t ≈ 3,7 ° C.

Khối lượng M của phần nước đá tan thành nước sau khi thả thỏi sắt nóng có nhiệt độ t ° C vào cốc nước đá ở 0 ° C được xác định bởi điều kiện cân bằng nhiệt:
M λ = cmt ⇒ M = cmt/ λ
trong đó λ là nhiệt nóng chảy riêng của nước đá, c là nhiệt dung riêng của thỏi sắt có khối lượng m.
Thay số, ta tìm được :
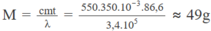

Gọi V là thể tích ở nhiệt độ t và V 0 là thể tích ở 0 ° C của thỏi sắt. Theo công thức nở khối vì nhiệt, ta có :
V = V 0 (1 + β t)
với β là hệ số nở khối của sắt. Vì khối lượng m của thỏi sắt không phụ thuộc nhiệt độ nên khối lượng riêng D của thỏi sắt ở nhiệt độ t liên hệ với khối lượng riêng D0 của nó ở 0oC theo công thức :
D/ D 0 = V 0 /V ⇒ D = m/V = D 0 /(1 + β t)
Từ đó suy ra nhiệt độ t của thỏi sắt trước khi thả nó vào cốc nước đá :
t = ( D 0 V - m)/m β
Thay số ta tìm được:
![]()

Lượng nhiệt cần cung cấp để biến đổi m = 6,0 kg nước đá ở nhiệt độ t 1 = -20 ° C biến thành hơi nước ở t 2 = 100 ° C có giá trị bằng :
Q = Q 1 + Q 2 + Q 3 + Q 4
trong đó lượng nhiệt Q 1 = c 1 m( t 0 - t 1 ) cung cấp cho m (kg) nước đá có nhiệt dung riêng c đ để nhiệt độ của nó tăng từ t 1 = -20 ° C đến t 0 = 0 ° C ; lượng nhiệt Q 0 = λ m cung cấp cho m (kg) nước đá có nhiệt nóng chảy riêng λ ở t 0 = 0 ° C tan thành nước ở cùng nhiệt độ ; lượng nhiệt Q 2 = c 0 m( t 2 - t 0 )
cung cấp cho m (kg) nước có nhiệt dung riêng c n để nhiệt độ của nó tăng từ t 0 = 0 ° C đến t 2 = 100 ° C ; lượng nhiệt Q 3 = Lm cung cấp cho m (kg) nước có nhiệt hoá hơi riêng L ở t 2 = 100 ° C biến thành hơi nước ở cùng nhiệt độ. Như vậy, ta có thể viết:
Q = c đ m( t 0 - t 1 ) + λ m + c n m( t 2 - t 0 ) + Lm
hay Q = m[ c đ ( t 0 - t 1 ) + λ + c n ( t 2 - t 0 ) + L]
Thay số, ta tìm được :
Q = 6,0. [2090.(0 + 20) + 3,4. 10 5 + 4180.(100 - 0) + 2,3. 10 6 ]
Q ≈ 186. 10 6 J.

Phương trình cân bằng nhiệt:
c m 2 ( t 2 - t ) = λ m 1 + c m 1 t ð t = c m 2 t 2 − λ m 1 c ( m 2 + m 1 ) = 7 ° C

Độ lớn của nhiệt lượng toả ra và nhiệt lượng thu vào :
Q t o ả = c 1 m 1 t 2 - t + c 2 m 2 t 2 - t = c 1 m 1 t 2 - t + c 2 M - m 1 t 2 - t (1)
Q t h u = c m t - t 1 + c 0 m 0 t - t (2)
Từ (1) và (2) dễ dàng tính được :
m 1 = 0,104 kg = 104 g ; m 2 = 0,046 kg = 46 g.

Đáp án: B
Phương trình cân bằng nhiệt:
cm2(t2 – t) = lm1 + cm1t
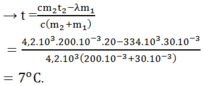
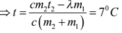
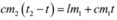
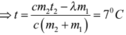
Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 , còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc đồng và của lượng nước đựng trong cốc.
- Lượng nhiệt do cốc đồng và lượng nước đựng trong cốc ở t 1 = 25 ° C toả ra để nhiệt độ giảm tới t = 15,2 ° C có giá trị bằng :
Q = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
- Lượng nhiệt do cục nước đá ở t 0 = 0 ° C thu vào để tan thành nước ở t = 15,2 ° C có giá trị bằng :
Q' = m 0 ( λ + c 2 t)
Theo nguyên lí cân bằng nhiệt, ta có :
Q' = Q ⇒ m 0 ( λ + c 2 t) = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
Từ đó suy ra :
Thay số với chú ý m0 = 0,775 - 0,700 = 0,075 kg, ta tìm được :