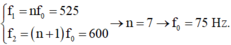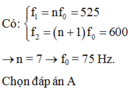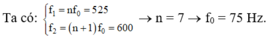Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Hai tần số liên tiếp trên dây cho sóng dừng, tương ứng với sóng dừng hình thành trên dây với n và n+1 bó sóng. Ta có:
l = n v 2 f n l = ( n + 1 ) v 2 f n + 1 ⇒ f n = n v 2 l f n + 1 = ( n + 1 ) v 2 l
⇒ f n + 1 - f n = v 2 l = f 0 = 200 - 150 = 50 Hz ⇒ v = 75 m / s .
với f0 là tần số nhỏ nhất gây ra sóng dừng trên dây (tương ứng với một bó sóng).

Đáp án C
Sóng dừng trên dây có hai đầu cố định có tần số f = n v 21
Theo bài ra ta có ( n + 1 ) v 21 - n v 21 = 200 - 150 → v 21 = 50
→ tốc độ truyền sóng trên dây là v = 50.2l = 50.2.0,75 = 75 m/s.

Chọn C
=>
F
o
= 84/6 hoac 98/7 (ứng với 1 bộ sóng giống âm chuẩn) = 14 Hz
Khi đó
l
=
λ
2
⇒
λ
-
2
l
=
1
,
2
m
=>
v
=
l
o
x
F
o
=
16
,
8
m
/
s

Chọn B
Điều kiện sóng dừng hai đầu cố định:
l
=
k
λ
2
=
k
v
2
⇒
k
v
=
1
,
6
f
Hai tần số gần nhau nhất cùng tạo sóng dừng trên dây thì số bó sóng hơn kém nhau là 1 nên ta có
k 1 , v = 1 , 6 f 1 , k 2 v = 1 , 6 f 2 ⇒ v = 1 , 6 f 2 - f 1 = 22 , 4 m / s

Đáp án A
Sóng dừng trên dây 2 đầu cố định nên ta có f = k v 2 L , suy ra f min = v 2 L ; f = k . f min
Theo đề bài: m . f min = 2964 n . f min = 4940 ⇒ f min = 2964 m f min = 4940 n ⇒ 4 , 1 < m < 7 , 8 6 , 9 < n < 13
Mặt khác: m n = 3 5 ⇒ m = 3 x , n = 5 x . Kết hợp với điều trên, ta có
4 , 1 < 3 x < 7 , 8 6 , 9 < 5 x < 13 ⇔ 1 , 3 < x < 2 , 6 1 , 38 < x < 2 , 6 ⇒ x = 2 , suy ra m = 6; n = 10 => f min = 494 (Hz).
Có 8000 ≤ 494 a ≤ 11000 ⇔ 16 , 1 ≤ a ≤ 22 , 2 . Suy ra có 6 giá trị a thỏa mãn, hay 6 giá trị tần số tạo ra sóng dừng thỏa mãn đề bài.