Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi alpha là góc hợp bởi mpn với mặt đất
\(\Rightarrow\sin\alpha=\dfrac{h}{l}=\dfrac{5}{10}=\dfrac{1}{2}\Rightarrow\alpha=30^0\)
\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{0}\Rightarrow F\cos30^0=mg\cos60^0\)
\(\Rightarrow A=F.\cos30^0.l=mg\cos60^0.l=100.10.\dfrac{1}{2}=...\left(J\right)\)
Ủa trường hợp a,b giống nhau mà :v?
\(l=10m\\ m=100kg\\ h=5m\\ \alpha=30^o\)
Trọng lượng của vật là:
\(P=m.g=100.10=1000\left(N\right)\)
a) Công tối thiểu cần thực hiện khi kéo kiện hàng bằng lực nằm ngang:
\(A=F.s=P.h=1000.5=5000\left(J\right)\)
b) Công tối thiểu cần thực hiện khi kéo kiện hàng theo phương hợp với mặt phẳng nghiêng \(30^o:\)
\(A'=F.s.\sin\alpha=P.h.\sin\alpha=1000.5.\sin30^o=2500\left(J\right)\)

Nếu đẩy hàng lên xe theo phương thẳng đứng thì lực tổng hợp bằng độ lớn của lực đẩy trừ đi trọng lực. Nếu đẩy hàng lên theo mặt phẳng nghiêng thì lực tổng hợp sẽ lớn hơn so với lực thành phần, vì vậy thùng hàng được đẩy lên dễ dàng hơn.

Nếu đẩy hàng lên xe theo phương thẳng đứng thì lực tổng hợp bằng độ lớn của lực đẩy trừ đi trọng lực. Nếu đẩy hàng lên theo mặt phẳng nghiêng thì lực tổng hợp sẽ lớn hơn so với lực thành phần, vì vậy thùng hàng được đẩy lên dễ dàng hơn.

Gọi m và m’ lần lượt là khối lượng của xe và của kiện hàng.
Chọn chiều dương là chiều chuyển động của xe
Áp dụng định luật II Niutơn:
cho xe: a 1 = F m (1)
cho xe và kiện hàng: a 2 = F m + m ' (2)
Quãng đường đi của xe trong hai trường hợp là
s = 1 2 a 1 t 1 2 = 1 2 a 2 t 2 2 (3)
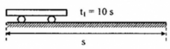
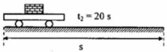
Từ (3), ta suy ra: a 1 a 2 = t 2 2 t 1 2 = 20 2 10 2 = 4
Từ (1) và (2), ta suy ra: a 1 a 2 = m + m ' m
→ m ' = 3 m = 3.50 = 150 k g
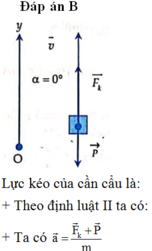
Đáp án: B

Tóm tắt: \(F=60N;m=20kg;F'=100N;g=10\)m/s2
\(\mu=?\)
Bài giải:
Ta có: \(\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Khi \(F=60N\) thì vật chuyển động đều\(\left(a=0\right)\):
\(\Rightarrow\mu.m.g=60\Rightarrow\mu.m=60:10=6\left(1\right)\)
Khi chất thêm một kiện hàng thì \(F'=100N\) vật chuyển động đều:
\(\Rightarrow\mu\left(m+20\right)g=100\Rightarrow\mu\left(m+20\right)=\dfrac{100}{10}=10\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\mu=0,2\)