K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

17 tháng 4 2017
Hướng dẫn trả lời:
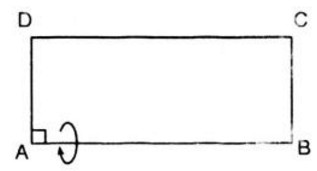
Theo đề bài ta có:
Diện tích hình chữ nhật ABCD là: AB.AD = 2a2 (1)
Chu vi hình chữ nhật là: 2(AB + CD) = 6a ⇒ AB + CD = 3a (2)
Từ (1) và (2), ta có AB và CD là nghiệm của phương trình:
x2 – 3ax – 2a2 = 0
Giải phương trình ta được x1 = 2a; x2 = a
Theo giả thiết AB > AD nên ta chọn AB = 2a; AD = a
Vậy diện tích xung quanh hình trụ là:
Sxq = 2π . AD . AB = 2π . a . 2a = 4 πa2
Thể tích hình trụ là:
V = π . AD2 . AB = π. a2 . 2a = 2πa3

CM
30 tháng 8 2018
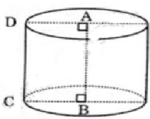
Theo đề bài ta có:
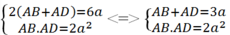
Coi AB và Ad như là các ẩn thì chungsex là các nghiệm của phương trình bậc hai:
![]()
(Tìm hai số khi biết tổng và tích của chúng).
Giải phương trình bận hai này ta có:
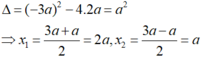
AB = 2a VÀ d = A (vì AB>AD)

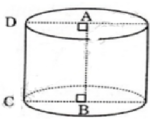

Người ta cuộn tấm bìa cát-tông hình chữ nhật có kích thước 4cm và 2cm thành hình trụ như hình vẽ. Tính diện tích xung quanh hình trụ?Diện tích xung quanh hình trụ là : .... cm2.
:43)
Người ta cuộn tấm bìa cát-tông hình chữ nhật có kích thước 4cm và 2cm thành hình trụ như hình vẽ. Tính diện tích xung qu
Hình đâu bạn ?