NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
16 tháng 5 2021
Đặt \(t=x^2\left(t\ge0\right)\)
pttt:\(t^2-mt+m+3=0\) (*)
Để pt ban đầu có 4 nghiệm pb <=> pt (*) có hai nghiệm t dương
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m-12>0\\m>0\\m+3>0\end{matrix}\right.\)\(\Leftrightarrow m>6\) (1)
Hai nghiệm nhỏ nhất của phương trình ban đầu có dạng \(-\sqrt{t_1},-\sqrt{t_2}\)
Có \(-\sqrt{t_1}-\sqrt{t_2}< -3\)
\(\Leftrightarrow t_1+t_2+2\sqrt{t_1t_2}>9\)
\(\Leftrightarrow m+2\sqrt{m+3}>9\)
\(\Leftrightarrow2\sqrt{m+3}>9-m\)
TH1: \(9-m< 0\Leftrightarrow m>9\) (2)
TH2: \(\left\{{}\begin{matrix}9-m\ge0\\4\left(m+3\right)>81-18m+m^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le9\\m\in\left(11-2\sqrt{13};11+2\sqrt{13}\right)\end{matrix}\right.\)
\(\Leftrightarrow m\in\left[11-2\sqrt{13};9\right]\backslash\left\{11-2\sqrt{13}\right\}\) (3)
Từ (1) (2) (3) => m>6
Ý B
4 tháng 3 2021
Câu 1:
Ta có: \(\Delta=\left[-2\left(m+2\right)\right]^2-4\cdot m\cdot\left(2+3m\right)\)
\(\Leftrightarrow\Delta=\left(2m+4\right)^2-4m\left(2+3m\right)\)
\(\Leftrightarrow\Delta=4m^2+16m+16-8m-12m^2\)
\(\Leftrightarrow\Delta=-8m^2+8m+16\)
\(\Leftrightarrow\Delta=-8\left(m^2-m-2\right)\)
Để phương trình vô nghiệm thì \(\Delta< 0\)
\(\Leftrightarrow m^2-m-2>0\)
\(\Leftrightarrow\left(m-2\right)\left(m+1\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m-2>0\\m+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}m-2< 0\\m+1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m>2\\m>-1\end{matrix}\right.\\\left\{{}\begin{matrix}m< 2\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\)
4 tháng 3 2021
Câu 1
Để pt vô nghiệm \(\Rightarrow\Delta'=\left(m+2\right)^2-\left(3m+2\right)m=m^2+4m+4-3m^2-2m=-2m^2+2m+4=-2\left(m^2-m-2\right)=-2\left(m+1\right)\left(m-2\right)< 0\) \(\Leftrightarrow\left(m+1\right)\left(m-2\right)>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>2\end{matrix}\right.\)
CM
22 tháng 7 2017
Phương trình có hai nghiệm
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
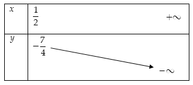
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B
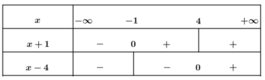
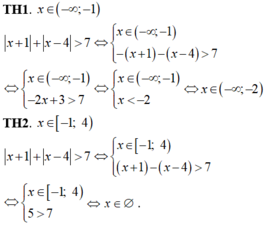
Phương trình này vô nghiệm