
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

Câu 1:
Đặt \(\sqrt{lnx+1}=t\Rightarrow lnx=t^2-1\Rightarrow\frac{dx}{x}=2tdt\)
\(\Rightarrow I=\int3t.2t.dt=6\int t^2dt=2t^3+C\)
\(=2\sqrt{\left(lnx+1\right)^3}+C=2\left(lnx+1\right)\sqrt{lnx+1}+C\)
\(=ln\left(x.e\right)^2\sqrt{ln\left(x.e\right)+0}\Rightarrow a=2;b=0\)
Câu 2:
\(\int\limits^b_ax^{-\frac{1}{2}}dx=2x^{\frac{1}{2}}|^b_a=2\left(\sqrt{b}-\sqrt{a}\right)=2\Rightarrow\sqrt{b}-\sqrt{a}=1\)
Ta có hệ: \(\left\{{}\begin{matrix}\sqrt{b}-\sqrt{a}=1\\a^2+b^2=17\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4\\a=1\end{matrix}\right.\) (lưu ý loại cặp nghiệm âm do \(\frac{1}{\sqrt{x}}\) chỉ xác định trên miền (a;b) dương)
Câu 4:
\(\int\frac{3x+a}{x^2+4}dx=\frac{3}{2}\int\frac{2x}{x^2+4}dx+a\int\frac{1}{x^2+4}dx\)
\(=\frac{3}{2}ln\left(x^2+4\right)+\frac{a}{2}arctan\left(\frac{x}{2}\right)+C\)
\(\Rightarrow a=2\)
\(\Rightarrow I=\int\limits^{\frac{e}{4}}_1ln\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{x}dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.lnx|^{\frac{e}{4}}_1-\int\limits^{\frac{e}{4}}_1dx=\frac{e}{4}.ln\left(\frac{e}{4}\right)-\frac{e}{4}+1=-\frac{ln\left(2^e\right)}{2}+1\)
Câu 5:
\(f'\left(x\right)=\int f''\left(x\right)dx=-\frac{1}{4}\int x^{-\frac{3}{2}}dx=\frac{1}{2\sqrt{x}}+C\)
\(f'\left(2\right)=\frac{1}{2\sqrt{2}}+C=2+\frac{1}{2\sqrt{2}}\Rightarrow C=2\)
\(\Rightarrow f'\left(x\right)=\frac{1}{2\sqrt{x}}+2\)
\(\Rightarrow f\left(x\right)=\int f'\left(x\right)dx=\int\left(\frac{1}{2\sqrt{x}}+2\right)dx=\sqrt{x}+2x+C_1\)
\(f\left(4\right)=\sqrt{4}+2.4+C_1=10\Rightarrow C_1=0\)
\(\Rightarrow f\left(x\right)=2x+\sqrt{x}\)
\(\Rightarrow F\left(x\right)=\int f\left(x\right)dx=\int\left(2x+\sqrt{x}\right)dx=x^2+\frac{2}{3}\sqrt{x^3}+C_2\)
\(F\left(1\right)=1+\frac{2}{3}+C_2=1+\frac{2}{3}\Rightarrow C_2=0\)
\(\Rightarrow F\left(x\right)=x^2+\frac{2}{3}\sqrt{x^3}\Rightarrow\int\limits^1_0\left(x^2+\frac{2}{3}\sqrt{x^3}\right)dx=\frac{3}{5}\)

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

1. \(f\left(x\right)=e^{x^3-3x+3}\) trên đoạn \(\left[0;2\right]\)
Ta có : \(f'\left(x\right)=\left(3x^2-3\right)e^{x^3-3x+3}=0\Leftrightarrow3x^2-3=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\notin\left[0;2\right]\\x=1\in\left[0;2\right]\end{array}\right.\)
mà : \(\begin{cases}f\left(0\right)=e^3\\f\left(1\right)=e\\f\left(2\right)=e^5\end{cases}\) \(\Rightarrow\begin{cases}Max_{x\in\left[0;2\right]}f\left(x\right)=e^5;x=1\\Min_{x\in\left[0;2\right]}f\left(x\right)=e;x=2\end{cases}\)
2. \(f\left(x\right)=\ln\left(x^2-x+1\right)\) trên đoạn \(\left[1;3\right]\)
Mà \(\begin{cases}f\left(1\right)=0\\f\left(3\right)=\ln7\end{cases}\) \(\Leftrightarrow\begin{cases}Max_{x\in\left[1;3\right]}f\left(x\right)=\ln7;x=3\\Min_{x\in\left[1;3\right]}f\left(x\right)=0;x=1\end{cases}\)
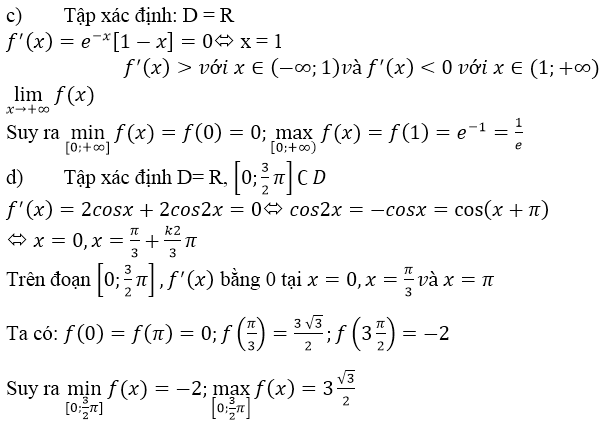
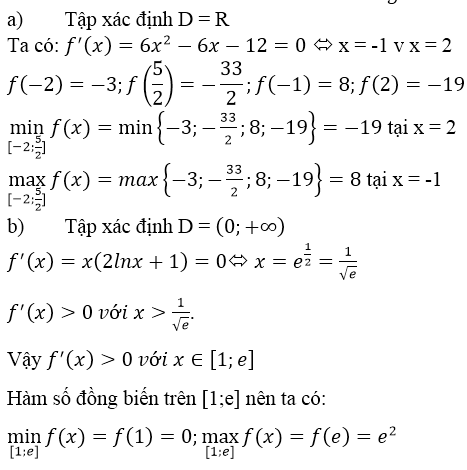
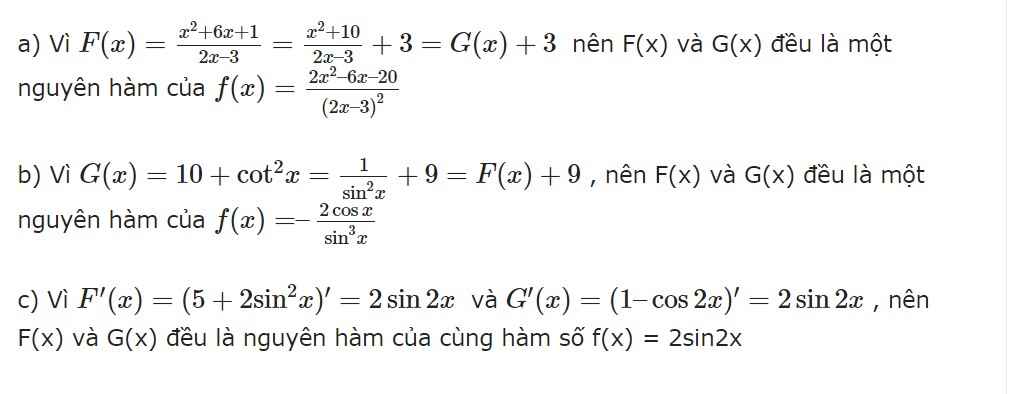
Chọn C
∫ 1 x - 1 d x = ln x - 1 + C
Vì F ( 2 ) = 1 nên C = 1.
Vậy F ( x ) = ln x - 1 + 1 , thay x = 3 ta được F(3) = ln2 + 1