
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
|
a.a. Hai đường tròn (I;R)(I;R) và (I′;R′)(I′;R′) tiếp xúc ngoài với nhau, ta xét : *Trường hợp 1:1: Nếu R=R′R=R′ thì k=±1k=±1 Khi đó, tâm vị tự OO thỏa mãn : OI′−→−=kOI−→⇒kOI′→=kOI→⇒k chỉ có thể bằng −1−1 ⇒O⇒O (tâm vị tự trong) là trung điểm của II′II′ (chính là tiếp điểm của hai đường tròn) *Trường hợp 2:2: Nếu R≠R′R≠R′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn I′;R′I′;R′ và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→IA→ và I′A′−→−I′A′→ cùng hướng - Đường thẳng II′II′ cẳt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong và O2O2 trùng với tiếp điểm) b.b. Hai đường tròn (I;R),(I′;R′)(I;R),(I′;R′) tiếp xúc trong với nhau (R≠R′)(R≠R′) ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng. - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) c.c. Đường tròn (I;R)(I;R) nằm trong đường tròn (I′;R′)(I′;R′) ta xét : *Trường hợp 1: Nếu I≡I′I≡I′ thì khi đó tâm vị tự OO trùng với điểm II Vậy ta có hai phép vị tự : - Phép vị tự V1(I;k1)V1(I;k1) với k1=R′Rk1=R′R (biến điểm MM thành điểm M′1M1′) - Phép vị tự V2(I;k2)V2(I;k2) với k2=−R′Rk2=−R′R (biến điểm MM thành điểm M′2M2′) *Trường hợp 2:2: Nếu II không trùng với I′I′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) |
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
|
a.a. Hai đường tròn (I;R)(I;R) và (I′;R′)(I′;R′) tiếp xúc ngoài với nhau, ta xét : *Trường hợp 1:1: Nếu R=R′R=R′ thì k=±1k=±1 Khi đó, tâm vị tự OO thỏa mãn : OI′−→−=kOI−→⇒kOI′→=kOI→⇒k chỉ có thể bằng −1−1 ⇒O⇒O (tâm vị tự trong) là trung điểm của II′II′ (chính là tiếp điểm của hai đường tròn) *Trường hợp 2:2: Nếu R≠R′R≠R′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn và là một bán kính của sao cho hai véctơ IA−→IA→ và I′A′−→−I′A′→ cùng hướng - Đường thẳng II′II′ cẳt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong và O2O2 trùng với tiếp điểm) b.b. Hai đường tròn (I;R),(I′;R′)(I;R),(I′;R′) tiếp xúc trong với nhau (R≠R′)(R≠R′) ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng. - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) c.c. Đường tròn (I;R)(I;R) nằm trong đường tròn (I′;R′)(I′;R′) ta xét : *Trường hợp 1: Nếu I≡I′I≡I′ thì khi đó tâm vị tự OO trùng với điểm II Vậy ta có hai phép vị tự : - Phép vị tự V1(I;k1)V1(I;k1) với k1=R′Rk1=R′R (biến điểm MM thành điểm M′1M1′) - Phép vị tự V2(I;k2)V2(I;k2) với k2=−R′Rk2=−R′R (biến điểm MM thành điểm M′2M2′) *Trường hợp 2:2: Nếu II không trùng với I′I′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) |

Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8

Gọi hai đường tròn lần lượt là (I; R) và (I’; R’).
Các xác định tâm vị tự của hai đường tròn:
- Trên đường tròn (I; R) lấy điểm M bất kì.
- Trên đường tròn (I’; R’) dựng đường kính AB // IM.
- MA và MB lần lượt cắt II’ tại O1 và O2 chính là hai tâm vị tự của hai đường tròn.
Đối với từng trường hợp ta xác định được các tâm vị tự O1; O2 như hình dưới.
+ Hình 1.62a:
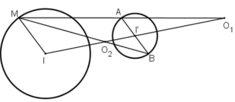
+ Hình 1.62b:
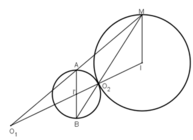
+ Hình 1.62c.
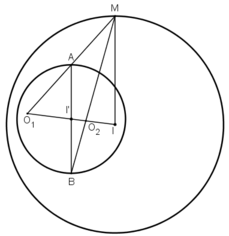

Dễ thấy bán kính của (C') bằng 4. Tâm I' của (C') là ảnh của tâm I(1;2) của (C) qua phép đồng dạng nói trên. Qua phép vị tự tâm O, tỉ số \(k=-2,I\) biến thành \(I_1\left(-2;-4\right)\). Qua phép đối xứng qua trục \(Ox\), \(I_1\) biến thành \(I'\left(-2;4\right)\).
Từ đó suy ra phương trình của (C') là \(\left(x+2\right)^2+\left(y-4\right)^2=16\)
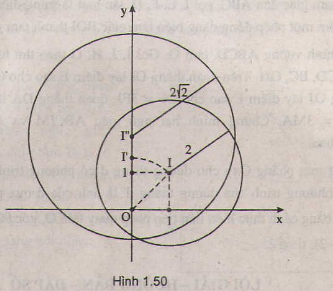
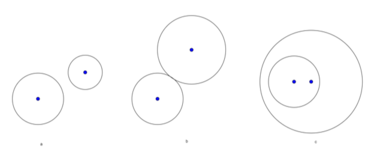



Gọi hai đường tròn là (I1: R1) và (I2; R2).
+ TH1: I1 ≡ I2; khi đó tâm vị tự O ≡ I1 ≡ I2; tỉ số vị tự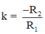 biến đường tròn (I1; R1) thành đường tròn (I2; R2).
biến đường tròn (I1; R1) thành đường tròn (I2; R2).
+ TH2: I1 ≠ I2.
Vẽ bán kính I1M bất kì.
Dựng đường kính AB của (I2; R2) sao cho AB // I1M.
MA; MB lần lượt cắt I1I2 tại O1 và O2.
Khi đó O1 và O2 chính là hai tâm vị tự của hai đường tròn.