Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M=8^10+4^10/8^4+4^11
=(2^3)^10+(2^2)^10/(2^3)^4+(2^2)^11
=2^30+2^20/2^12+2^22
=2^(30+20)/2^(12+22)
=2^50/2^34
=2^16
mik lm xog r nha

\(\frac{13}{38}>\frac{13}{39}\) => \(\frac{13}{38}>\frac{1}{3}\)
\(\frac{12}{37}<\frac{12}{36}\) => \(\frac{12}{37}<\frac{1}{3}\)
=> 13/38 > 12/37

`\color{blue}\text {#DuyNam}`
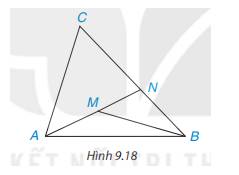
`NA` là đường trung tuyến
`-> A` là trung điểm của `MP`
`-> MA =AP`
`PB` là đường trung tuyến
`-> B` là trung điểm của `MN`
`-> MB=BN`
Vì Tam giác `MNP` cân tại `M`
`-> MN=MP,`\(\widehat{N}=\widehat{P}\)
`-> MB=MA=BN=AP`
Xét Tam giác `NAP` và Tam giác `PBN:`
`BN = AP`
\(\widehat{N}=\widehat{P}\)
`NP` chung
`=>` Tam giác `NAP =` Tam giác `PBN (c-g-c)`
`-> NA=PB (2` cạnh tương ứng `)`
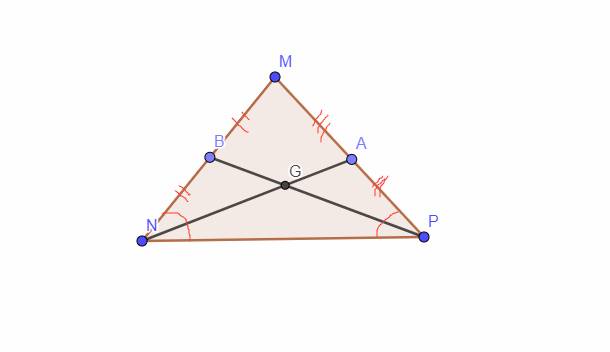

ΔDEF=ΔMNP
nên DE=MN; EF=NP; DF=MP
EF+FD=10 nên NP+MP=10
mà NP-MP=2
nên NP=6; MP=4
DE=MN=3cm
NP=EF=6cm
MP=DF=4cm

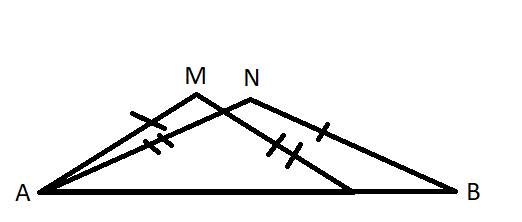
a) 3 điểm M,N,B không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác MNB có:
MB < MN + NB
MA + MB < MA + MN + NB
MA + MB < NA + NB ( vì MA + MN = NA) (1)
b) 3 điểm A,N,C không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác ACN có:
NA < CA + CN
NA + NB < CA + CN + NB
NA + NB < CA + CB ( vì CN + NB = CB) (2)
c) Từ (1) và (2) ta có:
MA + MB < NA + NB < CA + CB
Vậy MA + MB < CA + CB

Từ 2x = 3y = -2z suy ra \(\frac{2x}{1}=\frac{3y}{1}=\frac{2z}{-1}\)
\(=\frac{2x}{1}=\frac{3y}{1}=\frac{4z}{-2}=\frac{2x-3y+4z}{1-1+\left(-2\right)}=\frac{48}{-2}=-24\)
Với \(\frac{2x}{1}=-24\Rightarrow x=-12\)
Với \(\frac{3y}{1}=-24\Rightarrow y=-8\)
Với \(\frac{4z}{-2}=-24\Rightarrow z=12\)
Vì 2x = 3y = -2z nên -3y = -2x , 4z = -4x
=> 2x-3y+4z = 2x-2x-4x = 48 <=> x = -12
=> y = -8 ; z = 12