Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Năng lượng của electron ở trạng thái dừng n là \(E_n = -\frac{13,6}{n^2}.(eV)\)
\(hf_1 =\frac{hc}{\lambda_1}= E_3-E_1.(1) \)
\(hf_2 =\frac{hc}{\lambda_2}= E_5-E_2.(2) \)
Chia hai phương trình (1) và (2): \(\frac{\lambda_2}{\lambda_1}= \frac{E_3-E_1}{E_5-E_2}.(3)\)
Mặt khác: \(E_3-E_1 = 13,6.(1-\frac{1}{9}).\)
\(E_5-E_2 = 13,6.(\frac{1}{4}-\frac{1}{25}).\)
Thay vào (3) => \(\frac{\lambda_2}{\lambda_1}= \frac{800}{189}\) hay \(189 \lambda_2 = 800 \lambda_1.\)

Đáp án C
Nguyên tử có thể phát ra phôtôn có năng lượng lớn nhất bằng với năng lượng nó vừa hấp thụ.

Khi electron chuyển từ L (n = 2) sang K (n = 1) phát ra phô tôn có bước sóng λ21 thỏa mãn:
\(\frac{hc}{\lambda_{21}}= E_2-E_1,(1)\)
Tương tự
\(\frac{hc}{\lambda_{32}}= E_3-E_2,(2)\)
\(\frac{hc}{\lambda_{31}}= E_3-E_1,(3)\)
Cộng (2) cho (1), so sánh với (3):
\(\frac{hc}{\lambda_{21}}+\frac{hc}{\lambda_{32}}= \frac{hc}{\lambda_{31}}\)=> \(\frac{1}{\lambda_{31}}=\frac{1}{\lambda_{21}}+\frac{1}{\lambda_{32}} \)
=> \(\lambda_{31}= \frac{\lambda_{32}\lambda_{21}}{\lambda_{32}+\lambda_{21}}.\)

\(E_n = -\frac{13,6}{n^2},(eV)\)(với n = 1, 2, 3,..)
Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng 2,55 eV.
Việc đầu tiên là cần phải xác định xem nguyên tử nhảy từ mức nào lên mức nào mà có hiệu năng lượng giữa hai mức đúng bằng 2,55 eV.
\(E_1 = -13,6eV\), \(E_3 = -1,51 eV\)
\(E_2 = -3,4eV\),\(E_4 = -0,85eV\)
Nhận thấy \(E_4-E_2= -0,85 +3,4= 2,55 eV.\)
Như vậy nguyên tử đã hấp thụ năng lượng và nhảy từ mức n = 2 lên mức n = 4.
Tiếp theo, nguyên tử đang ở mức n = 4 rồi thì nó có thể phát ra bước sóng nhỏ nhất ứng với từ n = 4 về n = 1 tức là \(\lambda_{41}\) thỏa mãn
\(\lambda_{41}= \frac{hc}{E_4-E_1}= \frac{6,625.10^{-34}.3.10^8}{(-0,85+13,6).1,6.10^{-19}}=9,74.10^{-8}m. \)
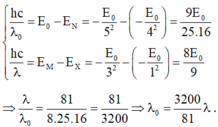
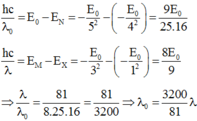
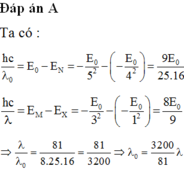


Chọn D