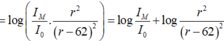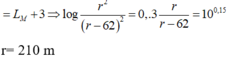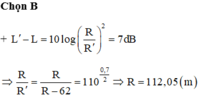Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

\(L_A=10lg\left(\frac{I_A}{I_0}\right)\Rightarrow I_A=0,1\left(Wm^2\right)\)

Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B

Gọi I là cường độ âm tại M và I' là cường độ âm tại điểm ở gần hơn, ta có :
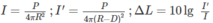
do đó
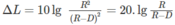
Với ∆ L = 7dB, D = 62m ta được:
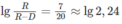
Do đó R = 2,24D/1,24 = 56.62/31 = 112m

Đáp án: B
HD Giải:
L + 6 - L = 10 lg I ' I
<=> 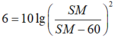
<=> SM = 120,3m