Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

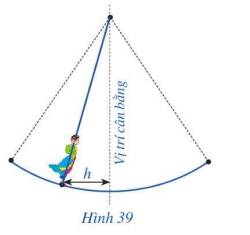
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.
Khi đó
\(\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t - 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t - 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}\)
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.
Khi đó
\(\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}\)

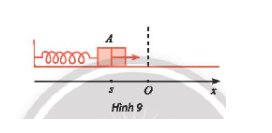
Vật đi qua vị trí cân bằng thì x = 0
Khi đó
\(\begin{array}{l}2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\\Leftrightarrow t = \frac{2\pi }{15} + \frac{{k\pi }}{5} ;k \in Z\end{array}\)
Do khoảng thời gian từ 0 đến 6 giây nên \(t \in \left[ {0;6} \right]\)
\(\begin{array}{l}0 \le \ \frac{{2\pi }}{{15}} + \frac{{k\pi }}{5} \le \ 6;k \in Z\\ \Rightarrow \frac{-2 }{3}\le \ k \le \ \frac{90 - 2\pi}{3\pi};k \in Z\end{array}\)
Do \(k \in Z\) nên \(k \in \left\{ {0;1;2;3;4;5;6;7;8} \right\}\)
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.

Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.

Đáp án B
Số phần tử không gian mẫu bằng 7 3 và số kết quả thuận lợi cho biến cố bằng 7.6.5
và xác suất cần tính bằng 7 . 6 . 5 7 3 = 30 49

* 7.7.7 = 73 = 343
* \(A\frac{3}{7}=210\)
Do đó : \(P\left(A\right)=\frac{210}{343}=\frac{30}{49}\)
cậu giải được bài này thì cậu học 11 = tuổi Bình , vậy sao xưng chị (phía trên )?+!
Sách Giải Bài Tập Toán Lớp 11 Luyện Tập (trang 46-47) (Nâng Cao)
Tham khảo.
https://sachgiaibaitap.com/sach_giai/giai-toan-lop-11-nang-cao-luyen-tap-trang-46-47/