Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Gọi x 0 ≤ x ≤ 8 ; x ∈ Z là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là 10(6x+10)=60x+100 nghìn đồng.
Chi phí vận hành 50x nghìn đồng.
Số bản in trong một giờ là 3600x suy ra thời gian để in xong 50000 tờ quảng cáo là 50000 3600 x = 125 9 x giờ
Vậy tổng chi phí là f x = 60 x + 100 25 9 x + 50 x nghìn đồng
Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.
Thay các giá trị x = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ta thấy giá trị nhỏ nhất là f 5 = 12250 9 .

Đáp án C
Giả sử có n máy thì chi phí cố định là
50 n n = 1 ; 2 ; 3...8
Để in 50000 tờ cần 5000 3600. n = 125 9 n (giờ in).
Chi phí cho n máy chạy trong một giờ là 10 6 n + 10 nghìn đồng.
Khi đó, tổng chi phí để in 50000 tờ quảng cáo là:
f n = 50 n + 10 6 n + 10 .125 9 n = 450 n 2 + 7500 n + 1250 9 n
( Đến đây các em có thể thay 4 giá trị xem giá trị nào cho kết quả nhỏ nhất).
Ta có: f ' n = 0 ⇔ n = 5 3 10 ≈ 5 , 27
Lại có: f 5 < f 6 nên ta cần sử dụng 5 máy để chi phí nhỏ nhất.

Chọn A.
Phương pháp: Lập hàm số và tìm giá trị min.

Chi phi để bảo dưỡng và giám sát máy in là:
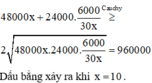

Đáp án A
Từ giả thiết ta có x + y = 10 và tổng tiền lãi nhận được là T = x 3 + 2 x + 326 y − 7 y 2
Khi đó:
T = x 3 + 2 x + 326 10 − x − 7 10 − x 2 = x 3 − 27 x 2 + 216 x + 560
Xét hàm số f x = x 3 − 27 x 2 + 216 x + 560 với x ∈ 0 ; 10 , có f ' x = 3 x 2 − 54 x + 216
Phương trình:
f ' x = 0 ⇔ 0 < x < 10 x 2 − 18 x + 72 = 0 ⇔ x = 6 ⇒ max f x = f 6

Gọi x, y, z là khối lượng gạo mỗi máy đã xay, ta có
x/(3*5*1/4) = y/(4*6*1/3) = z/(5*7*1/2)
x/(15/4) = y/8 = z/(35/2) = (x + y + z)/(15/4 + 8 + 35/2)
Biết x + y + z = 585, suy ra
x/(15/4) = y/8 = z/(35/2) = 585/(117/4) = 20
Vậy
x = (15/4)*20 = 075 tấn
y = . . . 8*20 = 160 tấn
z = (35/2)*20 = 350 tấn

Đáp án C
Gọi f n là hàm chi phí in 50000 tờ quảng cáo 0 < n ≤ 8 ; n ∈ ℕ . Ta cần tìm n để f(n) có giá trị thấp nhất. Theo giả thiết f(n) bao gồm chi phí vận hành cho n máy là 50n nghìn đồng. Và chi phí chạy máy sản xuất 50000 tờ quảng cáo là: 50000 3600 n 10 6 n + 10 = 2500 9 n 3 n + 5
Vậy f ( n ) = 50 n + 2500 9 n 3 n + 5 = 50 n + 250 9 n + 2500 3
Đến đây ta có thể khảo sát hàm f(n) với nnguyên để tìm chi phí thấp nhất hoặc kiểm tra trực tiếp bốn đáp án và được kết quả thấp nhất với n=5.