Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x (km) là độ dài quãng đường AB, y (giờ) là thời gian dự định đi để đến B đúng lúc 12 giờ trưa.
Điều kiện x > 0, y > 1 (do ôtô đến B sớm hơn 1 giờ).
+ Với v = 35km/h thì thời gian đi hết quãng đường AB là : t =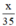 
(giờ)
Ô tô đến chậm hơn 2 giờ so với dự định ⇒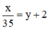 
⇔ x = 35y + 70.
+ Với v = 50 km/h thì thời gian đi hết quãng đường AB là :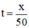 
(giờ)
Ô tô đến sớm hơn 1h so với dự định ⇒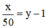 
⇔ x = 50y – 50.
- Gọi x (km) là quãng đường dài AB , y (giờ) là thời gian dự định đi từ A để đến B lúc 12h trưa .
đk : x > 0 , y > 1 ( vì ô tô đến B sớm hơn 1h )
Ta có 2TH sau :
+) TH1 :
- Xe đi với vận tốc 35km/h
- Xe đến B chậm hơn 2 giờ nên thời gian đi hết là : y + 2 ( giờ )
- Quãng đường đi được là : 35(y+2) (km)
=> Quãng đường không đổi nên ta có PT : x = 35(y+2) (1)
+) Trường hợp 2:
Xe đi với vận tốc: 50 km/h
Vì xe đến B sớm hơn 1 giờ nên thời gian đi hết là: y−1 (giờ)
Quãng đường đi được là: 50(y−1) (km)
Vì quãng đường không đổi nên ta có phương trình: x = 50(y−1)) (2)
Từ (1) và (2) ta có hệ phương trình :
\(\hept{\begin{cases}x=35\left(y+2\right)\\x=50\left(y-1\right)\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=35y+70\\x=50y-50\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-35y=70\left(1\right)\\x-50y=-50\left(2\right)\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}15y=120\\x-50y=-50\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=8\\x=-50+50y\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=8\\x=-50+50.8\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=8\\x=350\end{cases}\left(TM\right)}\)
Vậy quãng đường AB là 350km.
Thời điểm xuất phát của ô tô tại A là: 12 − 8 = 4 giờ
Gọi x (km) là độ dài quãng đường Ab, y (giờ) là thời gian dự định đi để đến B đúng lúc 12 giờ trưa. Điều kiện x > 0, y > 1 (do ôtô đến B sớm hơn 1 giờ).
Thời gian đi từ A đến B với vận tốc 35km là \(\frac{x}{35}\) = y + 2.
Thời gian đi từ A và B với vận tốc 50km là \(\frac{x}{50}\) = y - 1.
Ta có hệ phương trình: <=>\(\int^{\frac{x}{35}=y+2}_{\frac{x}{50}=y-1}\Leftrightarrow\int^{x=35\left(y+2\right)}_{y=50\left(y-1\right)}\)
Giải ra ta được: x = 350, y = 8.
Vậy quãng đường AB là 350km.
Thời điểm xuất phát của ô tô tại A là: 12 - 8 = 4 giờ.
Gọi x (km) là độ dài quãng đường Ab, y (giờ) là thời gian dự định đi để đến B đúng lúc 12 giờ trưa. Điều kiện x > 0, y > 1 (do ôtô đến B sớm hơn 1 giờ).
Thời gian đi từ A đến B với vận tốc 35km là \(\frac{x}{35}\) = y + 2.
Thời gian đi từ A và B với vận tốc 50km là \(\frac{x}{50}\) = y - 1.
Ta có hệ phương trình: <=>\(\int^{\frac{x}{35}=y+2}_{\frac{x}{50}=y-1}\Leftrightarrow\int^{x=35\left(y+2\right)}_{y=50\left(y-1\right)}\)
Giải ra ta được: x = 350, y = 8.
Vậy quãng đường AB là 350km.
Thời điểm xuất phát của ô tô tại A là: 12 - 8 = 4 giờ.
Gọi thời gian dự kiến mà xe ô tô sẽ đi từ A đến B là x(h)
(ĐIều kiện: x>0)
Độ dài quãng đường AB khi xe đi với vận tốc 35km/h là:
35(x+2)(km)
Độ dài quãng đường AB khi xe đi với vận tốc 50km/h là:
50(x-1)(km)
Do đó, ta có phương trình:
35(x+2)=50(x-1)
=>10(x-1)=7(x+2)
=>10x-10=7x+14
=>3x=24
=>x=8(nhận)
Thời điểm xuất phát của ô tô là:
12 giờ-8 giờ=4 giờ
Độ dài quãng đường AB là:
35(8+2)=35*10=350(km)
Gọi vận tốc của xe lúc đầu là x (km/h) , chiều dài quãng đường AB là y (km) (x>10,y>0)
Theo đề bài :
Xin lỗi mình còn thiếu:
Hệ hương trình : \(\hept{\begin{cases}\frac{y}{x+10}=\frac{y}{x}-3\\\frac{y}{x-10}=\frac{y}{x}+5\end{cases}}\)
Giải ra được : x = 40 (TM) , y = 600 (TM)
Vậy vận tốc lúc đầu của xe là 40 km/h
Thời gian dự định là 15 giờ
Chiều dài quãng đường là 600 km
Gọi vận tốc dự định là x
Theo đề, ta có: \(\dfrac{90}{x-10}-\dfrac{90}{x}=\dfrac{3}{4}\)
=>90x-90(x-10)=3x(x-10)
=>x(x-10)=30x-30(x-10)=300
=>x^2-10x-300=0
=>x=60
t k biết