Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường AB cần đi là x (km) (Điều kiện x thuộc N*)
với vận tốc là 45 km/h thì đến sớm 2h
=> đến đúng giờ sẽ là \(\dfrac{S}{45}+2\) (h)
còn với vận tốc 54 km/h thì đến sớm 3h
=> đến đúng giờ sẽ là \(\dfrac{S}{54}+3\)
Theo bài ra, ta có phương trình:
\(\dfrac{S}{45}+2=\dfrac{S}{54}+3\) <=> \(\dfrac{6S+540}{270}=\dfrac{5S+810}{270}\)
=> 6S+540=5S+810
<=>S=810-540=270 (Thỏa mãn)
Vậy quãng đường AB là 270km.

Tham khảo:
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ
Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)
Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)
Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)
Như vậy hàm số tính quãng đường s (km) sau t phút là:
\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)
b)
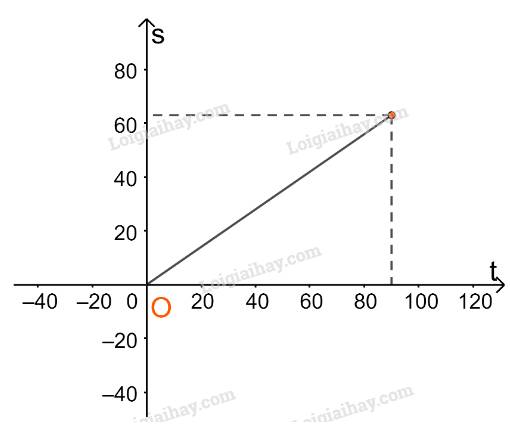
Với \(0 \le t \le 90\) thì \(s = 0,7t\)
Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)
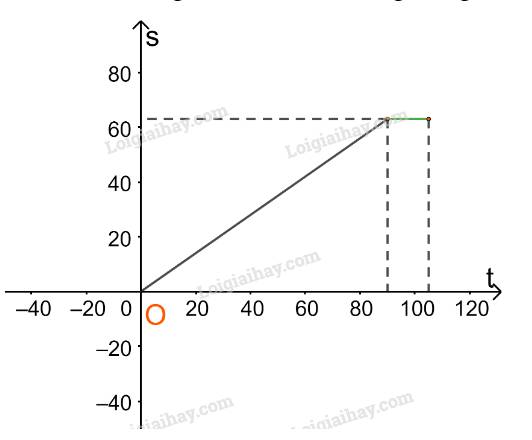
Với \(90 < t \le 105\) thì \(s = 63(km)\)
Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)
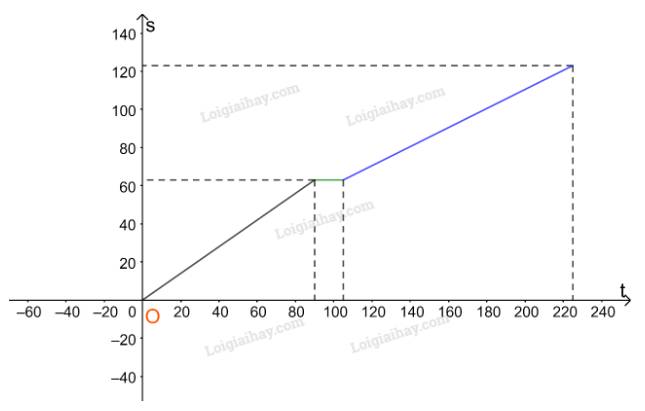
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

Thời gian ô tô đi Từ A đến B là :
180:90=2(giờ)
Vì ô tô nghỉ tại B 30 phút=0,5 giờ nên sau 2,5 h ô tô bắt đầu từ B quay về A
Lúc 8h xe đạp bắt đầu đi từ A đến B.vì xe đạp đi muộn hơn 1 h nên lúc ô tô bắt đầu quay lại A thì xe đạp đi được1,5 giờ nên được quãng đường là:
1,5x15=22,5 km
Thời gian 2 xe gặp nhau là:
(180-22,5):(90+15)=1,5 giờ
Vậy 2 xe gặp nhau lúc: 7h+2,5h+1,5h=11 giờ
Điểm gặp nhau cách A số km là:
1,5x15 +22,5=45km

Gọi x, y > 0 (km/giờ)lần lượt là vận tốc trung bình lúc đi và vận tốc trung bình lúc về.
Theo đề bài ta có hệ phương trình:
y − x = 20 175 x + 175 y = 6 ⇔ y = 20 + x ( 1 ) 175 x + 175 y = 6 ( 2 )
Thế (1) vào (2) ta được:
175 x + 175 20 + x = 6 ⇔ 6 x 2 − 230 x − 3500 = 0 ⇔ x = 50 x = − 35 3 ⇔ x = 50 vì x>0
Vận tốc lúc đi là 50 km/giờ
Đáp án cần chọn là: D

Gọi một phần là a ta có:
Chiều rộng là 3a
Chiều dài là 4a
Diện tích hình chữ nhật là:
3a x 4a = 12a2 = 437,4
=> a2 = 36,45
=> a = 6
Vậy ta có :
Chiều dài hình chữ nhật đó là :
6 x 4 = 24 ( cm )
Chiều rộng hình chữ nhật đó là :
6 x 2 = 12 ( cm )
Đáp số : Chiều dài hình chữ nhật đó là : 24 cm
Chiều rộng hình chữ nhật đó là : 12 cm

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

Gọi vận tốc dự định của Nam là x km/h(x>0)
Quãng đường AB dài là: 5x(km)
Vận tốc thực của Nam là: x-8(km/h)
Thời gian Nam đi với vận tốc thực là 7 giờ nên:
\(\frac{5x}{x-8}\)=7
5x=7(x-8)
5x=7x-56
2x=56
x=56:2
x=28 km/h
Vậy vận tốc thực của Nam là: 28-8=20km/h
Quãng đường AB dài là: 5x28=140 km
chiều dài xe buýt là 15m