Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(S_1=50m\)
\(v_2=10m\)/s
\(S_2=130m\)
\(t_1=t_2\)
\(v_1=?\)
------------------------------------------
Bài làm:
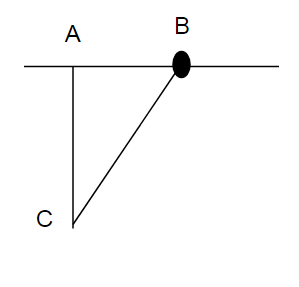
50m130mACB
Gọi vị trí hai người gặp nhau là:C và vị trí của xe khách là:B
Áp dụng định lí Py-ta-go vào \(\Delta vABC\) có:
\(BC^2=AB^2-AC^2\)
\(\Rightarrow BC^2=130^2-50^2=14400\)
\(\Rightarrow BC=\sqrt{14400}=120m\)
Thời gian xe khách đi đến C là:
\(t_2=\dfrac{S_{BC}}{v_2}=\dfrac{120}{10}=12\left(s\right)\)
Vận tốc của người đó có thể gặp xe là:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{50}{12}\approx4,17\left(m\text{/}s\right)\)
Vậy ...............................

Thế thì khi ta đứng trong tàu hoả đang chạy với tốc độ cao, sau khi nhảy lên, có phải ta cũng vẫn rơi xuống chỗ cũ như vậy chăng?
Có thể có người nghĩ như thế này: Tàu hoả đang chạy với tốc độ cao, trong quãng thời gian sau khi con người nhảy lên, tàu hoả đã chạy được một đoạn, con người phải rơi xuống ở chỗ lùi lại một ít. Tàu hoả chạy càng nhanh, khoảng cách so với chỗ cũ sau khi rơi xuống càng xa. Song sự thực cho chúng ta biết: Khi tàu hoả đang chạy với tốc độ cao, sau khi nhảy lên vẫn rơi đúng vào chỗ cũ. Vì sao lại như thế nhỉ?
Nguyên nhân là bất cứ vật thể nào cũng đều có quán tính. Chuyển động của vật thể phải tuân theo định luật quán tính. Nội dung của định luật quán tính (tức là định luật thứ nhất của Newton): Trong điều kiện không chịu tác động của ngoại lực, trạng thái chuyển động của vật thể sẽ không thay đổi. Khi tàu hoả đang chạy với tốc độ cao, cho dù con người đứng yên, nhưng trên thực tế người ấy đã lao về phía trước cùng với tàu hoả, với cùng một tốc độ như của tàu hoả. Khi người ấy nhảy lên, vẫn lao về phía trước cùng tàu hoả với cùng một tốc độ. Vì vậy, khi người ấy rơi xuống vẫn là chỗ cũ.
Đã từng có người nghĩ ra một ý “”tuyệt diệu””. Anh ta nói: chỉ cần tôi ngồi lên khí cầu bay lên cao, do sự tự quay của Trái Đất, tôi có thể trông thấy mặt đất ở phía dưới dịch chuyển nhanh chóng. Nếu bay lên từ Thượng Hải, dừng ở trên không khoảng một giờ rưỡi rồi lại hạ xuống, chẳng phải là đã đến thành La Sa của Khu tự trị Tây Tạng hay sao? Rõ ràng đó là chuyện không thể xảy ra. Vì rằng mọi vật xung quanh Trái Đất như con người, khí cầu, không khí… đều quay cùng Trái Đất mà!
Không nơi nào là không có quán tính. Khi một chiếc ô tô đang chạy rất nhanh, bỗng nhiên phanh gấp lại, người trong xe đều bị xô về phía trước, khi xe bỗng nhiên khởi động, người trong xe lại ngả về phía sau. Đó đều là do quán tính.”

1) ĐỀ NÊN LÀ 2 NGƯỜI XUẤT PHÁT TỪ 2 ĐIỂM KHÁC NHAU.
Bài làm:
Gọi s1; s2; s lần lượt quãng đường người đi vận tốc
Hai người gặp nhau khi: \(s=s_1+s_2\)
\(\Leftrightarrow\left(v_1+v_2\right)t=s\)
\(t=\dfrac{s}{v_1+v_2}=\dfrac{2,5}{10+15}=0,1h\)
Điểm này cách A một khoảng: \(s_3=v_1t=10.0,1=1km\)
Bài 1:
Tóm tắt:
\(s_{AB}=2,5km\\ v_1=10km|h\\ v_2=15km|h\\ \overline{t_g=?}\\ s_{g\rightarrow A}=?\)
Giải:
Gọi tg là thời gian di chuyển đến khi hai người gặp nhau.
Quãng đường người thứ nhất di chuyển đến lúc gặp nhau là:
\(s_1=v_1.t_g=10t_g\)
Quãng đường người thứ hai di chuyển cho đến lúc gặp nhau là:
\(s_2=v_2.t_g=15.t_g\)
Ta có:
\(s_1+s_2=s_{AB}\\ \Leftrightarrow10t_g+15t_g=2,5\\ \Leftrightarrow t_g\left(10+15\right)=2,5\\\Leftrightarrow t_g=\dfrac{2,5}{25}=0.1 \)
Vị trí hai người gặp nhau so với điểm A là:
\(s_{g\rightarrow A}=v_1.t_g=10.0,1=1\left(km\right)\)
Vậy thời gian để hai người gặp nhau là 0,1h
Khoảng cách từ vị trí hai người gặp nhau đến A là 1km

Gọi S là quãng đường ô tô đi đến chỗ người đón.
\(S_1\) là khoảng cách chỗ người đó đang đứng đến nới ô tô đang đứng.
\(S_2\) là khoảng cách từ chỗ người đó đến quãng đường.
\(\Rightarrow S=\sqrt{S_1^2-S_2^2}=\sqrt{206^2-100^2}=6\sqrt{901}m\)
\(v=36\)km/h=10m/s
Thời gian ô tô đi đến chỗ đón:
\(t=\dfrac{S}{v}=\dfrac{6\sqrt{901}}{10}=18s\)
Vận tốc đi để vừa gặp ô tô là:
\(v'=\dfrac{S_1}{t}=\dfrac{100}{18}=5,55\)m/s

ta có:
gọi t' là tổng thời gian đi trên nửa quãng đường cuối
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\) (*)
ta lại có:
thời gian đi trên nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{60}\left(1\right)\)
tổng quãng đường lúc sau là:
\(S_2+S_3=\frac{S}{2}\)
\(\Leftrightarrow v_2t_2+v_3t_3=\frac{S}{2}\)
\(\Leftrightarrow25t_2+15t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{25t'+15t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow40t'=S\Rightarrow t'=\frac{S}{40}\left(2\right)\)
lấy (1) và (2) thế vào phương trình (*) ta có:
\(v_{tb}=\frac{S}{\frac{S}{60}+\frac{S}{40}}=\frac{S}{S\left(\frac{1}{60}+\frac{1}{40}\right)}=\frac{1}{\frac{1}{60}+\frac{1}{40}}=24\)
vậy vận tốc trung bình của người này là 24km/h
trong 1/2 thời gian đầu người ấy đi được:
\(S''=\frac{t}{2}.v_{tb}=\frac{v_{tb}\left(t_1+t'\right)}{2}\)
\(\Leftrightarrow S''=\frac{24\left(\frac{S}{60}+\frac{S}{40}\right)}{2}\)
\(\Leftrightarrow S''=\frac{24\left(\frac{2S+3S}{120}\right)}{2}\)
\(\Leftrightarrow S''=\frac{\left(\frac{120S}{120}\right)}{2}\)
\(\Leftrightarrow S''=\frac{S}{2}\)
mình làm vậy bạn xem đúng ko nhé![]()