Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.

Đáp án A
*Trong một chu kì lò xo có nén chứng tỏ A > ∆ l o

Chú ý: Lực kéo lớn nhất khi vật ở vị trí thấp nhất (tức là vị trí lò xo giãn nhiều nhất). Lực nén lớn nhất khi vật ở vị trí cao nhất (tức là lò xo bị nén nhiều nhất).

Đáp án A
Trong một chu kì lò xo có nén chứng tỏ

Chú ý: Lực kéo lớn nhất khi vật ở vị trí thấp nhất (tức là vị trí lò xo giãn nhiều nhất). Lực nén lớn nhất khi vật ở vị trí cao nhất (tức là lò xo bị nén nhiều nhất).

Đáp án A
Chu kì dao động của con lắc lò xo T = 2 π ∆ l 0 g = 0,4 s
Ta có:
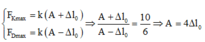
Khoảng thời gian lò xo bị nén trong một chu kỳ ∆ t = T π a r cos ∆ l 0 A = 0 , 168 s

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Đáp án B