Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
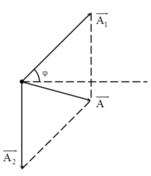
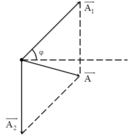
Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
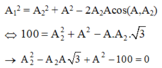
Phương trình trên luôn có nghiệm nên:


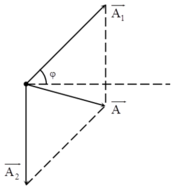
- Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
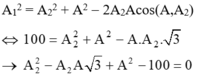
- Phương trình trên luôn có nghiệm nên:
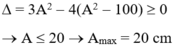
- Với: 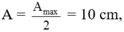
thay vào phương trình trên ta được: 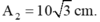

$x_1$ vuông pha với $x_2$ $\Rightarrow $$x_{12}$=$\sqrt{16^2+A_2^2}$
Đề không tồn tại sự tổng hợp dao động này thì $A_{123}$ max < 25cm
$\Rightarrow $ $16^2$+$A_2^2$+25+2.5.$\sqrt{16^2+A_2^2}$ < $25^2$
$\sqrt{16^2+A_2^2}$<20$\Rightarrow $ $A_2$ < 12
Chọn B.

Đáp án D
+ Ta có:
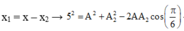
![]()
→ Để phương trình có nghiệm A2 thì ∆ = 3 A 2 - 4 ( A 2 - 25 ) ≥ 0 → A m a x = 10 cm
→ Với A = 0,5Amax = 5 cm → A 2 = 5 3 c m

+ Ta có x1 = x – x2
![]()
![]()
→ Để phương trình có nghiệm A2 thì
![]()
→ Với A = 0,5Amax = 5 cm
![]()

Đáp án D

Theo định lý hàm sin: A sin α = 5 sin 30 ⇒ A = 10 sin α
Giá trị max của A = 10 c m nếu sin α = 1 . Đề bài yêu cầu A bằng 1 nửa giá trị này, tức là sin α = 0 , 5 . Lúc đó α = 30 ° .
Áp dụng định lý hàm cosin cho tam giác:
A 2 2 = 5 2 + 5 2 − 2.5.5. c os 120 ⇒ A 2 = 5 3 ( c m )

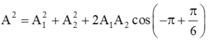
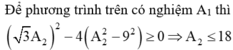

\(x_1 = 5 \cos (\omega t + \varphi)cm.\)
\(x_2 = A_2 \cos (\omega t - \frac{\pi}{4})cm.\)
\(x= A \cos (\omega t - \frac{\pi}{12})cm.\)
Vẽ giản đồ véc tơ như hình vẽ
A 2 A A 1 0 φ π/6 -π/4 -π/12 3π/4-φ 3π/4-φ
Áp dụng định lý hàm số Sin ta có:
Xét: \(\triangle OA_1A:\) \(\frac{A}{\sin OA_1A} = \frac{A_1}{\sin OAA_1} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_1}{\sin (\frac{\pi}{6})} \)
=> \(A= \frac{A_1}{\sin (\frac{\pi}{6})} .\sin (\frac{3\pi}{4}-\varphi).(*)\)
TH1: \(A= A _{max} <=> \sin (\frac{3\pi}{4}-\varphi) = 1\)
=> \(A_{max}= \frac{A_1}{\sin (\frac{\pi}{6})}= 10cm.(1)\)
TH2: \(A = \frac{A_{max}}{2} => \sin (\frac{3\pi}{4}-\varphi) = \frac{1}{2}.\)
=> \(\frac{3\pi}{4} - \varphi = \frac{\pi}{6}\)
=> \(\varphi = \frac{7\pi}{12}.(2)\)
Xét: \(\triangle OA_2A:\) \(\frac{A}{\sin OA_2A} = \frac{A_2}{\sin OAA_2} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_2}{\sin (\varphi+\frac{\pi}{12})} \)
=> \(A_2= \frac{A_{max}}{\sin (\frac{3\pi}{4}-\varphi)} .\sin (\frac{\pi}{12}+\varphi).(3)\)
Thay \((1); (2)\) vào \((3)\) ta được: \(A_2= \frac{10}{0,5} .\sin (\frac{\pi}{12}+\frac{7\pi}{12}) = \frac{10}{0,5}.\frac{\sqrt{3}}{2} = 10 \sqrt{3}cm.\)
Chọn đáp án.C.\(10\sqrt{3}cm.\)
Bạn kiểm tra lại xem giả thiết còn thiếu gì không?