

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án D
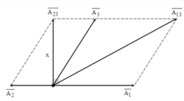
Biểu diễn vecto các dao động.
+ Ta có E 1 = 2 E 2 E 13 = 3 E 23 → A 1 = 2 A 2 A 13 = 3 A 23
Để đơn giản, ta chọn A 2 = 1 A 23 = x → A 1 = 2 A 13 = 3 x
+ Từ hình vẽ ta có 3 x 2 = x 2 + 1 + 2 2 → x = 1 + 2 2
Vì x 1 ⊥ x 23 nên biên độ của dao động tổng hợp của vật là A 2 = A 23 2 + A 1 2 = 1 + 2 2 2 + 2 2
→Ta có E E 23 = E W = A 2 A 23 2 = 1 + 2 2 2 + 2 2 1 + 2 2 2 ≈ 1 , 7

Đáp án D
Theo đề ta vẽ được giản đồ vecto như hình vẽ
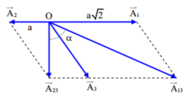
Ta có
![]()
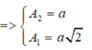
Từ hình vẽ ta có :
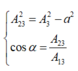
Theo đề
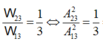
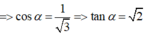
Lại có
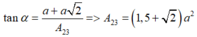
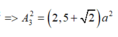
Vì
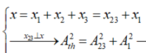
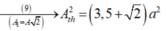
Ta có:
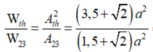
![]()

Giải:
\(W_1=2W_2\Rightarrow A_1=A_2\sqrt{2}=a\sqrt{2}\)
Đặt \(A_{23}=x\) thì: \(x_{23}\perp x_1\rightarrow x_{23}\perp x_2\Rightarrow A_3=\sqrt{x^2+a^2}\)
Ta lại có: \(A_{13}=\sqrt{A_1^2+A^2_3+2A_1A_3\cos\left(x_1;x_3\right)}\)
Trong đó: \(\cos\left(x_1;x_3\right)=-\cos\left(x_2;x_3\right)=\dfrac{a}{\sqrt{x^2+a^2}}\)
Do đó: \(A_{13}=\sqrt{x^2+3a^2+2\sqrt{2}a^2}\)
Kết hợp với giả thiết ta có:
\(3=\dfrac{W_{13}}{W_{23}}=\left(\dfrac{A_{13}}{A_{23}}\right)^2=\dfrac{x^2+3a^2+2\sqrt{2}a^2}{x^2}\)
\(\Rightarrow x=\dfrac{\sqrt{2}+1}{\sqrt{2}}a\)
Do \(x_{23}\perp x_1\) nên:
\(A_{th}=\sqrt{A^2_{23}+A^2_1}=\sqrt{2a^2+\dfrac{3+2\sqrt{2}}{2}a^2}\) \(=\dfrac{7+2\sqrt{2}}{\sqrt{2}}a\)
\(\Rightarrow\dfrac{W_{th}}{W_{23}}=\left(\dfrac{A_{th}}{A_{23}}\right)^2=...=\dfrac{7+2\sqrt{2}}{\sqrt{2}+1}\approx1,7\)
Vậy ta chọn \(D\)


![]()
![]()
Bình luận: Để nhanh chóng tìm được kết quả ta chuẩn hóa nhanh như sau
*Lập tỉ giữa 2 trong 3 phương trình trên ta được:
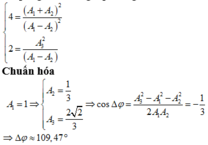

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

C. biên độ bằng hiệu hai biên độ của hai dao động thành phần

Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức